3x-1

It probably came into being between 3x-1 s and s. In his review paper, J.

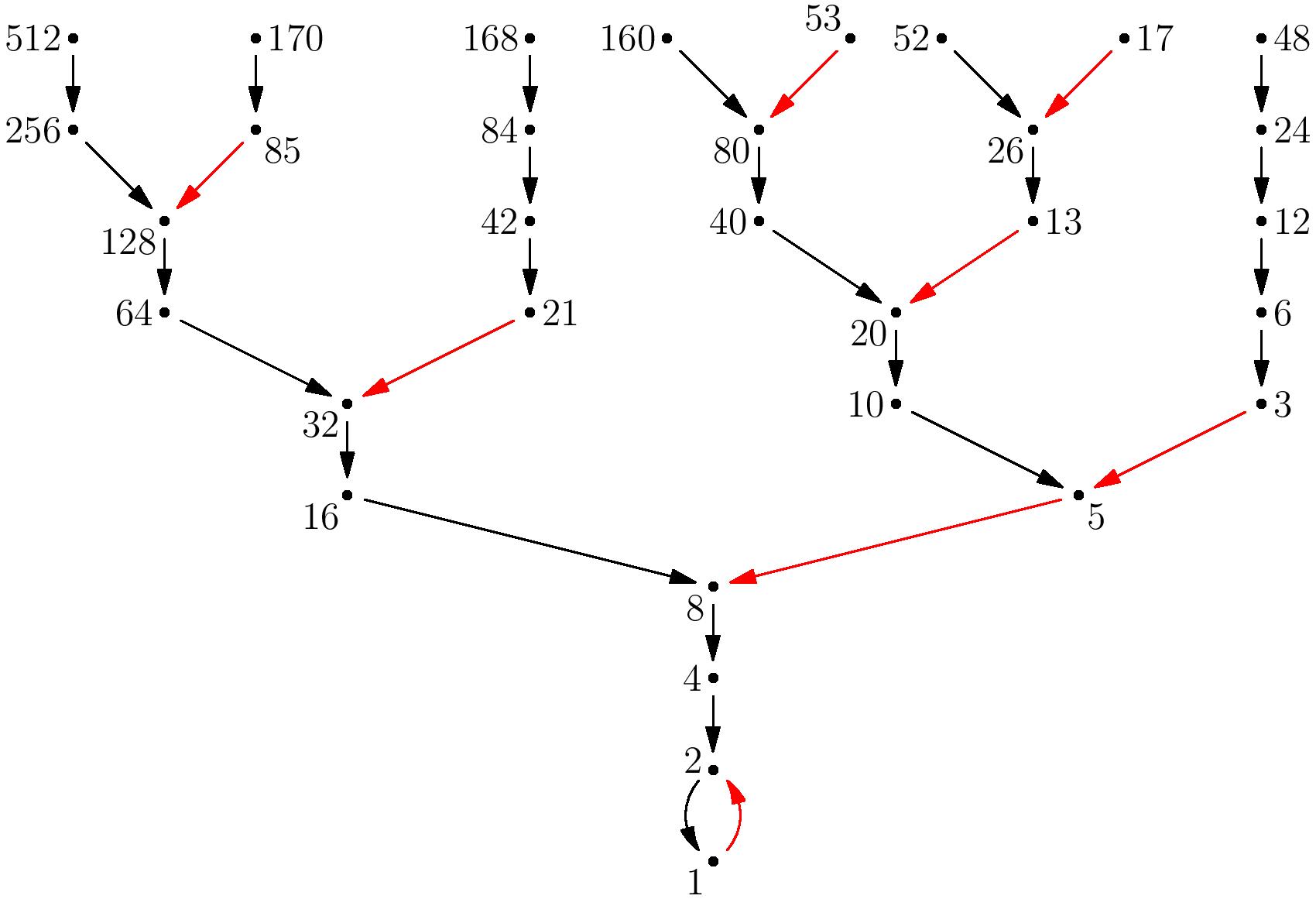
It is also known as the Collatz problem or the hailstone problem. This leads to the sequence 3, 10, 5, 16, 4, 2, 1, 4, 2, 1, A sequence obtained by iterating the function from a given starting value is sometimes called "the trajectory" of that starting value. Obviously there can be no consecutive odd numbers in any trajectory, but there may certainly be consecutive even numbers, especially when the trajectory reaches a power of 4, in which the trajectory quickly plummets to 1 after passing through all the intervening powers of 2. Note that since the odd-indexed powers of 2 are congruent to 2 modulo 3, they are only reachable from halving a power of 4. See also reduced Collatz function. Pure hailstone numbers are those which do not occur in the trajectories of smaller numbers, while impure hailstone numbers are those which do occur in the trajectories of smaller numbers.

3x-1

The Collatz conjecture [a] is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even , the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence. It is named after the mathematician Lothar Collatz , who introduced the idea in , two years after receiving his doctorate. Consider the following operation on an arbitrary positive integer :. Now form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next. The Collatz conjecture is: This process will eventually reach the number 1, regardless of which positive integer is chosen initially. If the conjecture is false, it can only be because there is some starting number which gives rise to a sequence that does not contain 1. Such a sequence would either enter a repeating cycle that excludes 1, or increase without bound. No such sequence has been found. The Collatz conjecture asserts that the total stopping time of every n is finite.

Letherman, 3x-1, Schleicher, and Wood extended the study to the complex plane. Search Advanced search.

.

Solve Practice Play. Game Central. Greatest Common Factor. Least Common Multiple. Order of Operations. Mixed Fractions. Prime Factorization. Solve for a Variable. Evaluate Fractions. Linear Equations.

3x-1

Please ensure that your password is at least 8 characters and contains each of the following:. Hope that helps! You'll be able to enter math problems once our session is over.

Dead by daylight board game

Theoretical Computer Science. In the movie Incendies , a graduate student in pure mathematics explains the Collatz conjecture to a group of undergraduates. They conjectured that the latter is not the case, which would make all integer orbits finite. Since this expression evaluates to zero for real integers, the extended function. No such sequence has been found. We proved lemma 4. The authors declare no conflicts of interest regarding the publication of this paper. What is not so obvious is whether every trajectory eventually reaches a power of 4. Forum of Mathematics, Pi. Although the conjecture has not been proven, most mathematicians who have looked into the problem think the conjecture is true because experimental evidence and heuristic arguments support it. Venturini, G.

A problem posed by L.

Up to now, many papers on this conjecture have been published at home and abroad [2] - [11], we can see from these papers [2] [3] [4] [5] that many people limited and stayed on the idea of function iteration. They conjectured that the latter is not the case, which would make all integer orbits finite. The same plot on the left but on log scale, so all y values are shown. So, instead of proving that all positive integers eventually lead to 1, we can try to prove that 1 leads backwards to all positive integers. A are. The number is taken to be 'odd' or 'even' according to whether its numerator is odd or even. DOI: Since the powers of two give an element of predictability, it is natural that a tree graph of Collatz sequences put the powers of two on the central axis, or at least line them up. Hidden category: Articles containing conjectures. So far, proposition 2 is proved. From then on, people rest assured to use it to understand and solve relevant problems. As proven by Riho Terras , almost every positive integer has a finite stopping time. For example, the parity cycle 1 0 1 1 0 0 1 has length 7 and four odd terms at indices 0, 2, 3, and 6. Lemma 2. The machine will perform the following three steps on any odd number until only one 1 remains:.