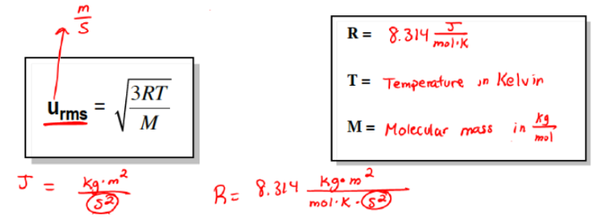
Root mean square speed

Gases are made up of individual atoms or molecules freely moving in random directions with a wide variety of speeds. Kinetic molecular theory tries to explain the properties of gases by investigating the behavior of individual atoms or molecules making up the gas. This example problem shows how to find the average or root mean square velocity rms of particles in a gas sample for a given temperature. Solution: Root root mean square speed square velocity is the average velocity of the molecules that make up a gas, root mean square speed.

Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq. Since N is the number of molecules and m is the mass of each molecule, Nm is the total mass of gas. The rms velocity is directly proportional to the square root of temperature and inversely proportional to the square root of molar mass. Thus quadrupling the temperature of a given gas doubles the rms velocity of the molecules.

Root mean square speed

We have examined pressure and temperature based on their macroscopic definitions. Pressure is the force divided by the area on which the force is exerted, and temperature is measured with a thermometer. We can gain a better understanding of pressure and temperature from the kinetic theory of gases , the theory that relates the macroscopic properties of gases to the motion of the molecules they consist of. First, we make two assumptions about molecules in an ideal gas. To derive the ideal gas law and the connection between microscopic quantities such as the energy of a typical molecule and macroscopic quantities such as temperature, we analyze a sample of an ideal gas in a rigid container, about which we make two further assumptions:. The collisions between molecules do not appear in the derivation of the ideal gas law. They do not disturb the derivation either, since collisions between molecules moving with random velocities give new random velocities. Furthermore, if the velocities of gas molecules in a container are initially not random and isotropic, molecular collisions are what make them random and isotropic. We make still further assumptions that simplify the calculations but do not affect the result. First, we let the container be a rectangular box. Second, we begin by considering monatomic gases, those whose molecules consist of single atoms, such as helium.

Measure advertising performance. Thus quadrupling the temperature of a given gas doubles the rms velocity of the molecules. So, if you take the individual speeds of a group of particles - square each one - add them up and then divide by the number of particles you are dealing with, you get the mean square speed - and that gives root mean square speed indication of absolute temperature.

This example problem demonstrates how to calculate the root mean square RMS velocity of particles in an ideal gas. This value is the square root of the average velocity-squared of molecules in a gas. While the value is an approximation, especially for real gases, it offers useful information when studying kinetic theory. What is the average velocity or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celsius? Gases consist of atoms or molecules that move at different speeds in random directions. The root mean square velocity RMS velocity is a way to find a single velocity value for the particles.

The laws that describe the behavior of gases were well established long before anyone had developed a coherent model of the properties of gases. In this section, we introduce a theory that describes why gases behave the way they do. The theory we introduce can also be used to derive laws such as the ideal gas law from fundamental principles and the properties of individual particles. The kinetic molecular theory of gases A theory that describes, on the molecular level, why ideal gases behave the way they do. Developed during the midth century by several physicists, including the Austrian Ludwig Boltzmann — , the German Rudolf Clausius — , and the Englishman James Clerk Maxwell — , who is also known for his contributions to electricity and magnetism, this theory is based on the properties of individual particles as defined for an ideal gas and the fundamental concepts of physics.

Root mean square speed

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Temperature, kinetic theory, and the ideal gas law. In a gas, there are lots of molecules traveling at lots of different speeds. Here's a framework for thinking about that.

Ny time zone est

Choose required ranks and required tasks. This is very different from the average speed Use limited data to select content. By Todd Helmenstine Todd Helmenstine. On the other hand, it is much greater than the typical difference in gravitational potential energy when a molecule moves from, say, the top to the bottom of a room, so our neglect of gravitation is justified in typical real-world situations. Archived from the original PDF on 15 January Strategy Identify the knowns and unknowns and determine which equations to use to solve the problem. Inception score FID. Coverage Intra-list Similarity. Square root of the mean square. This force is due to one molecule. In this equation alone, p represents momentum, not pressure.

This is the square root of the average mean of all of the square of the speeds of individual particles in a gas.

Thus the pressure quadruples. As a result, gas molecules escape very easily from the Moon, leaving it with virtually no atmosphere. The first option, speed equals zero, corresponds to the minimum of the distribution function. The mean square speed is proportional to absolute temperature. Because O 2 molecules are 16 times heavier than H 2 molecules, the average speed of H 2 molecules is 4 times faster. See also: Accuracy. Doubling this average velocity doubles the number of collisions between gas molecules and the walls of a container. The temperature must be converted to Kelvin and the molar mass must be found in kg to complete this problem. Similarly, if the average velocity of the molecules is higher, the gas pressure is higher. Note that the average kinetic energy of the molecule is independent of the type of molecule.