Derive lens makers formula

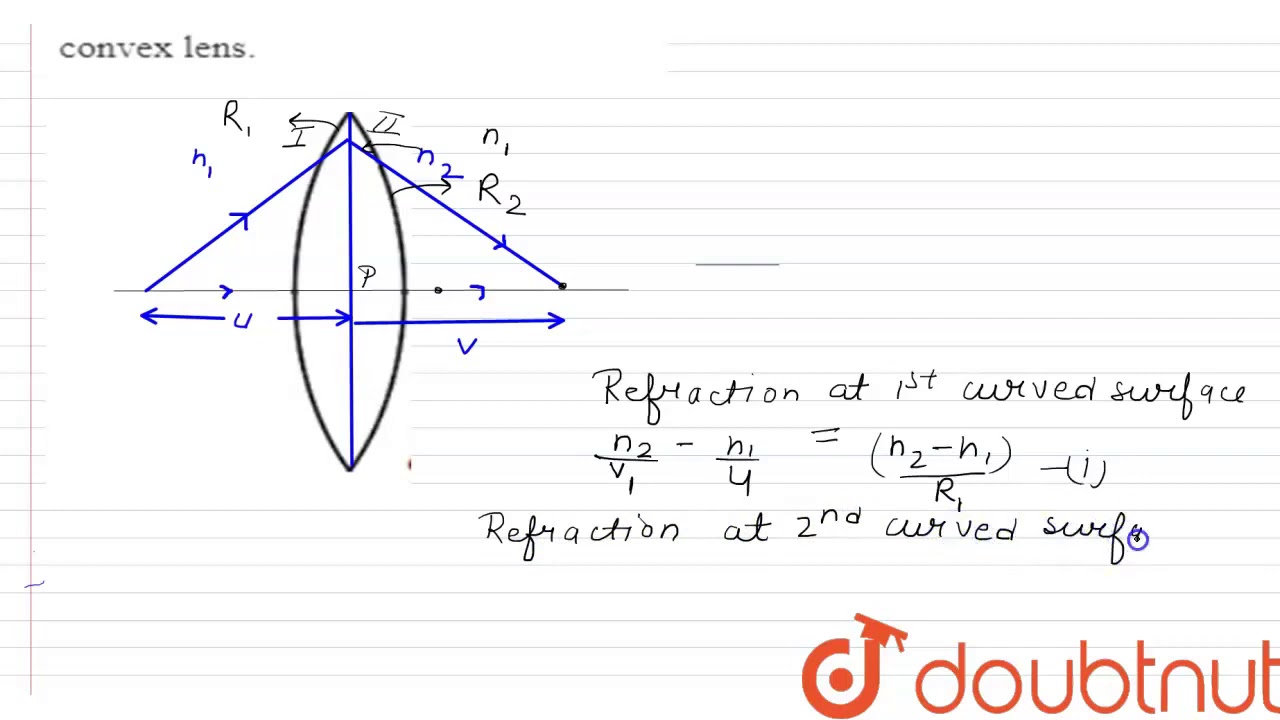
A lens is a transparent medium bounded by two curved surfaces usually spherical or cylindricalalthough one of the surfaces of the lens may be a plane, derive lens makers formula. The manufacturer of the lens selects the material of the lens and grinds its surface to make suitable radii of curvatures. He can therefore adjust the focal length of the lens.

Lenses of different focal lengths are used for various optical instruments. The derivation of lens maker formula is provided here so that aspirants can understand the concept more effectively. Lens manufacturers commonly use the lens maker formula for manufacturing lenses of the desired focal length. The complete derivation of the lens maker formula is described below. Using the formula for refraction at a single spherical surface, we can say that,. This is the lens maker formula derivation. Put your understanding of this concept to test by answering a few MCQs.

Derive lens makers formula

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Refraction in thin lenses. About About this video Transcript. Let's derive the famous lens makers formula. This formula only works for thin lenses. Created by Mahesh Shenoy. Want to join the conversation? Log in. Sort by: Top Voted. Posted 5 years ago. Downvote Button navigates to signup page. Flag Button navigates to signup page. Show preview Show formatting options Post answer.

The medium of both sides must be the same. We use ray tracing for thin lenses to illustrate how they form images, and then we develop equations to analyze quantitatively the properties of thin lenses.

However, not all lenses have the same shape. The vocabulary used to describe lenses is the same as that used for spherical mirrors: The axis of symmetry of a lens is called the optical axis, where this axis intersects the lens surface is called the vertex of the lens, and so forth. Likewise, a concave or diverging lens is shaped so that all rays that enter it parallel to its optical axis diverge, as shown in part b. To understand more precisely how a lens manipulates light, look closely at the top ray that goes through the converging lens in part a. Likewise, when the ray exits the lens, it is bent away from the perpendicular. The overall effect is that light rays are bent toward the optical axis for a converging lens and away from the optical axis for diverging lenses.

A lens is a transparent medium bounded by two curved surfaces usually spherical or cylindrical , although one of the surfaces of the lens may be a plane. The manufacturer of the lens selects the material of the lens and grinds its surface to make suitable radii of curvatures. He can therefore adjust the focal length of the lens. The lens maker's formula is a mathematical equation that relates the focal length of a thin lens to its refractive index and the radii of curvature of its two surfaces. It is given by the following equation:. The formula can be derived by considering the refraction of light through the lens. But before moving directly to the derivation part, first, have a brief review regarding the sign convention adopted and assumptions to be made while doing derivation, which can be found in the later parts of this article only. Example 1. A biconvex lens has radii of 20 cm each.

Derive lens makers formula

We will discuss the form of the equation that is applicable only to thin lenses. This formula is only applicable to a lens of a given refractive index placed in air. We make the assumption that this is a thin lens as stated earlier , the points D , P and E in figure 1 have a very small distance between them, which can be neglected. Therefore, the radii of curvature of the left side of the lens is the distance C 2 E, approximately the same as the C 2 P — i. Consider the lens setup as shown in Figure 2. O is the point at which the object is placed on the principal axis of the lens. The above figure shows the image formation at I. Let the distance between the center of the lens P and the object O be u units, and the distance PI is v units. The sign convention states that, 1.

Descendant dolls

The lens maker's formula is a mathematical equation that relates the focal length of a thin lens to its refractive index and the radii of curvature of its two surfaces. Although three rays are traced in this figure, only two are necessary to locate a point of the image. Test Series. The left-hand side looks suspiciously like the mirror equation that we derived above for spherical mirrors. Learning Objectives By the end of this section, you will be able to: Use ray diagrams to locate and describe the image formed by a lens Employ the thin-lens equation to describe and locate the image formed by a lens. Test your knowledge on Lens maker formula derivation Q 5. Note that the image is in focus but the face is not, because the image is much closer to the camera taking this photograph than the face. To understand more precisely how a lens manipulates light, look closely at the top ray that goes through the converging lens in part a. This is the thin-lens equation. Did not receive OTP? Are the signs correct? A ray entering a diverging lens parallel to the optical axis exits along the line that passes through the focal point on the same side of the lens ray 1 in part b of the figure. The medium used on both sides of the lens should always be the same. Clearly, we know that in a biconvex lens, the centre of curvature of the first surface is on the positive side of the lens and that of the second surface is on the negative side.

For a thin lens, the power is approximately the sum of the surface powers.

A lens is a transparent medium bounded by two curved surfaces usually spherical or cylindrical , although one of the surfaces of the lens may be a plane. Let us consider the thin lens shown in the image above with 2 refracting surfaces having the radii of curvatures R 1 and R 2 , respectively. I think you should probably learn the textbook one. The lens is thin. Search site Search Search. Example 1. Share Share Share Call Us. If the refraction Refractive index of the lens material is 1. Are the signs correct? Clearly, we know that in a biconvex lens, the centre of curvature of the first surface is on the positive side of the lens and that of the second surface is on the negative side. The figure shows three rays from many rays that emanate from the tip of the arrow. Properties Of Gravitational Force. Another important characteristic of thin lenses is that light rays that pass through the center of the lens are undeviated, as shown by light ray 2. Special lenses called doublets are capable of correcting chromatic aberrations. Likewise, a concave or diverging lens is shaped so that all rays that enter it parallel to its optical axis diverge, as shown in part b.