Volume of a square based pyramid formula

Here we will learn about the volume of a square based pyramid, including how to calculate the volume of a square based pyramid and how to solve problems involving the volume.

This volume of a pyramid with a square base calculator is easy to use and comes with explanations and instructions to help you with your square pyramid volume calculations. To find the volume of a pyramid with a square base, this calculator will be your best friend. All you need to do is enter any two measurements of your square pyramid into our calculator. In the next section of this text, we'll discuss the different square pyramid formulas we used to make this volume of a pyramid with a square base calculator work. The formula we use to find the volume of a square pyramid only uses two variables that we can easily measure on a pyramid. Those measurements are the base edge a and the height H of the pyramid, shown in the image below:.

Volume of a square based pyramid formula

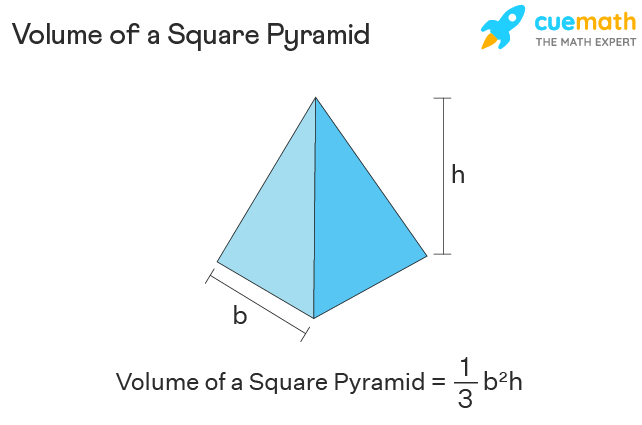
What do we mean by the volume of a square pyramid and how do we define it? Volume is nothing but the space that an object occupies. A square pyramid is a three-dimensional geometric shape that has a square base and four triangular bases that are joined at a vertex. Thus, the volume of a pyramid refers to the space enclosed between its faces. Let's learn how to find the volume of a square pyramid here with the help of few solved examples and practice questions. The volume of a square pyramid refers to the space enclosed between its five faces. The volume of a square pyramid is one-third of the product of the area of the base and the height of the pyramid. The volume of a square pyramid is the number of unit cubes that can fit into it and is represented in "cubic units". Commonly it's expressed as m 3 , cm 3 , in 3 , etc. A square pyramid is a three-dimensional shape with five faces. A square pyramid is a polyhedron pentahedron that consists of a square base and four triangles connected to a vertex. Its base is a square and the side faces are triangles with a common vertex.

The height of that triangle is the perpendicular height of the pyramid. Pyramid Image. Edit this Article.

This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon. This is also a right square pyramid where "right" refers to the fact that the apex lies directly above the centroid of the base. In other words the point at the top of the pyramid is directly above the center point of the square base.

The volume of a three-dimensional shape gives us an idea of the quantity of liquid it can hold or even the quantity of s pace it occupies. A three dimensional shape with four triangular lateral faces and a square base is known as a square pyramid. In this article, we will learn about the square pyramid and the volume of a square pyramid. Read More Read Less. A square pyramid is a three-dimensional geometrical shape with four lateral faces shaped as triangles, and a square base.

Volume of a square based pyramid formula

The volume of pyramid is space occupied by it or it is defined as the number of unit cubes that can be fit into it. A pyramid is a polyhedron as its faces are made up of polygons. There are different types of pyramids such as a triangular pyramid, square pyramid, rectangular pyramid, pentagonal pyramid, etc that are named after their base, i. All the side faces of a pyramid are triangles where one side of each triangle merges with a side of the base. Let us explore more about the volume of pyramid along with its formula, proof, and a few solved examples. The volume of a pyramid refers to the space enclosed between its faces. It is measured in cubic units such as cm 3 , m 3 , in 3 , etc. A pyramid is a three-dimensional shape where its base a polygon is joined to the vertex apex with the help of triangular faces. The perpendicular distance from the apex to the center of the polygon base is referred to as the height of the pyramid.

R navyblazer

How to calculate the volume of a square based pyramid. Thus, for a square pyramid, you only need to find the length of one side. Cookies make wikiHow better. A square based pyramid is a three dimensional shape made up of flat faces. Please log in with your username or email to continue. Find the side length, x of its square base. Assign variables. Terms and Conditions. Get a Widget for this Calculator. The volume of a square based pyramid can be found by using the formula. If you imagine cutting the pyramid diagonally from one corner to the opposite corner and opening it up, the exposed inside face is a triangle. We're glad this was helpful. Generally, units like cubic meters m 3 , cubic centimeters cm 3 , liters l , etc are the most common units used with the volume of the square pyramid. We can use this to find the perpendicular height of the pyramid.

In geometry, a square pyramid is a pyramid with a square base and four triangular lateral faces.

The square pyramid is a special case of a pyramid where the base is square. The volume of a square based pyramid can be found by using the formula. All Categories. In geometry, a square pyramid is a pyramid with a square base and four triangular lateral faces. Follow Us. Download Now. Privacy Policy. It is based on one of the pyramids of Giza. If you want to learn more about finding a square pyramid's height, you can check out our height of a square pyramid calculator. Multiply the area of the base by the pyramid's height. United States. Maths Program. It is possible to find the volume of a square pyramid using slant height, which means we can derive the formula for the volume of a square pyramid without height.