Sin a - sin b
Sin A - Sin B is an important trigonometric identity in trigonometry. It is used to find the difference of values of sine function for angles A and B. It is one of the difference to product formulas used to represent the difference of sine function for angles A and B into their product form. Let us study the Sin A - Sin B formula in detail in the following sections, sin a - sin b.
It is one of the sum to product formulas used to represent the sum of sine function for angles A and B into their product form. From this,. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Have a look at the below-given steps. Example 2: Using the values of angles from the trigonometric table , solve the expression: 2 sin Here, A and B are angles. Click here to check the detailed proof of the formula.
Sin a - sin b
The sum of two sines is equal to the cosine of their difference multiplied by the product of their amplitudes. The two sines are out of phase with each other if their difference is not an integer multiple of pi. In trigonometry, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. The tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side. This identity can be derived from first principles using the definition of sine and cosine. It can also be verified using basic algebraic manipulation. This identity is useful in solving problems involving angles that are not multiples of 90 degrees. For example, consider finding the value of sin 75 degrees without using a calculator. By applying the sin a sin b identity, we can break down this angle into two smaller angles: 60 degrees and 15 degrees. When two angles in a triangle have their sides opposite to each other equal in length, the triangle is said to be isosceles.
Maths Program.
When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B , and also equal to side c divided by the sine of angle C. The answers are almost the same! They would be exactly the same if we used perfect accuracy. Not really, look at this general triangle and imagine it is two right-angled triangles sharing the side h :. The sine of an angle is the opposite divided by the hypotenuse, so:. We can swing side a to left or right and come up with two possible results a small triangle and a much wider triangle. This only happens in the " Two Sides and an Angle not between " case, and even then not always, but we have to watch out for it.
Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here.
Sin a - sin b
The law of sines establishes the relationship between the sides and angles of an oblique triangle non-right triangle. Law of sines and law of cosines in trigonometry are important rules used for "solving a triangle". According to the sine rule, the ratios of the side lengths of a triangle to the sine of their respective opposite angles are equal. Let us understand the sine law formula and its proof using solved examples in the following sections. The law of sines relates the ratios of side lengths of triangles to their respective opposite angles. This ratio remains equal for all three sides and opposite angles. We can therefore apply the sine rule to find the missing angle or side of any triangle using the requisite known data.
Plaza premium lounge taipei terminal 2 review
Way to go ClubZ! Online Tutors. Properties as a function. Club Z! So there are two possible answers for R: The sum of two sines is equal to the cosine of their difference multiplied by the product of their amplitudes. Multiply both sides by 4. It can also be used to find an angle when two sides and one angle are known. Have a look at the below-given steps. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Thanks Z. Side a faces angle A, side b faces angle B and side c faces angle C. Online Tutors. Maths Program.
If you're seeing this message, it means we're having trouble loading external resources on our website.
We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Then, add these values together to get the final answer. Have a look at the below-given steps. Reduced trigonometric form. Global maxima. Multiplication Tables. Multiply both sides by 4. Alternate form. Explore math program. Click here to check the detailed proof of the formula. United Kingdom. Explore math program. Answer: 2 sin Working online with my tutor has been a piece of cake.

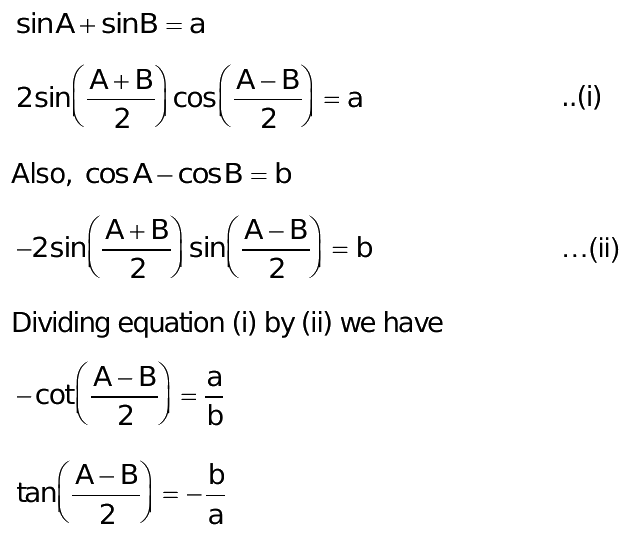
I apologise, but, in my opinion, you are not right. I am assured. I can defend the position. Write to me in PM.
Yes cannot be!