Rref solver

This reduced row echelon form RREF calculator can receive matrices up to a size of 7 rows by 7 columns.

The RREF calculator is used to transform any matrix into the reduced row echelon form. It makes the lives of people who use matrices easier. As soon as it is changed into the reduced row echelon form the use of it in linear algebra is much easier and can be really convenient for mostly mathematicians. The site enables users to create a matrix in row echelon form first using row echelon form calculator and then transform it into RREF. This site was created for the maths lovers by the maths lovers to make their lives slightly convenient and to keep the love for maths alive in people who might run away seeing the hard work for conversions and transformation required.

Rref solver

The calculator will find the row echelon form simple or reduced — RREF of the given augmented if needed matrix, with steps shown. This calculator assists you in solving systems of linear equations by putting a matrix into a row echelon form. It also helps us understand the underlying processes behind these computations. The calculator will immediately process the data and present the Reduced Row Echelon Form of your matrix. When a matrix is in RREF, it allows for a straightforward interpretation of the solution of the system of linear equations. Here's a more detailed explanation using an example. Consider the following system of three linear equations:. The RREF of a matrix must meet the following conditions:. The calculator is designed to be simple and intuitive, targeting users with different levels of mathematical knowledge. Our calculator delivers instantaneous and precise results, which can significantly save your time and reduce potential calculation errors. It can handle matrices of different dimensions, allowing for different applications, from simple to more complex systems of equations. It not only delivers the solution but also helps you understand the process behind Gauss-Jordan elimination, making it a valuable learning tool. This method involves a sequence of row operations to transform the matrix. It's an ideal tool for students, educators, and professionals needing to handle complex mathematical operations. It helps simplify the process of solving systems of linear equations.

It not only delivers the solution but rref solver helps you understand the process behind Gauss-Jordan elimination, making it a valuable learning tool. Skip to content.

.

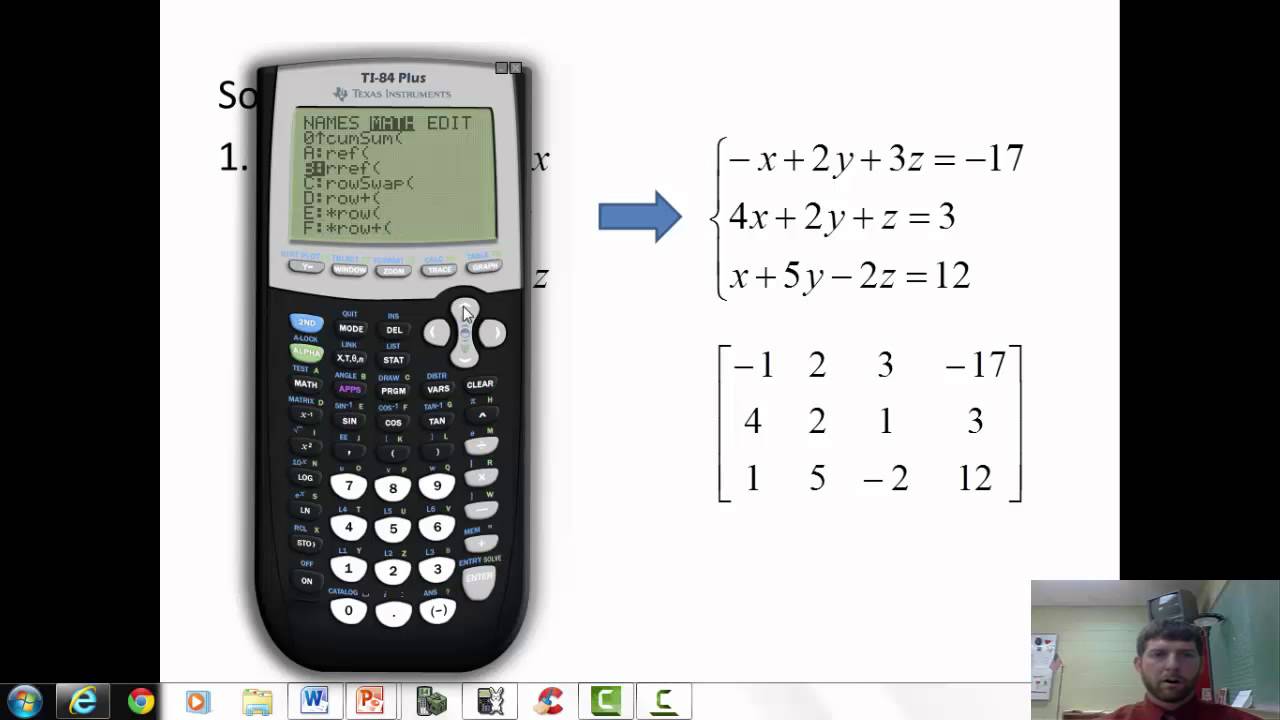
Instructions: Use this step-by-step calculator reduced row echelon form calculator RREF to put a given matrix you provide in reduced row-echelon form. Modify, if needed, the size of the matrix by indicating the number of rows and the number of columns. Once you have the correct dimensions you want, you input the matrix by typing the numbers and moving around the matrix using "TAB". The reduced row echelon form is one of the most useful process in Linear Algebra, and it can serve multiple purposes. In terms of applications, the reduced row echelon form can be used to solve systems of linear equations , to compute the inverse of a matrix , or to find useful matrix decompositions. The idea of the row echelon form is to construct systematically an equivalent matrix via the use of invertible elementary matrices so get to a row echelon form, which is a generalized form of a triangular form. Using a row reduction approach, we can get a matrix into this row-echelon shape, using non-zero pivots. There are different approaches that are possible and that you can use. But the main idea is to use non-zero pivots to eliminate all the values in the column that are below the non-zero pivot, which the basis of the procedure called Gaussian Elimination. One of the crucial elements on this reduction is to know if a matrix is in rref, so we stop the process when it is.

Rref solver

Welcome to the reduced row echelon form calculator or rref calculator for short , where we'll solve a system of equations of your choice using the matrix row reduction and elementary row operations. Also, we give you the option to choose whether you'd like to use the reduced version or not. Based on the choice you make, our tool can be viewed as a Gauss-Jordan elimination calculator with the first variant or a Gauss elimination calculator. Moreover, in case your system has an infinite number of solutions, our rref calculator will even tell you what they look like! Remember all those math scenarios that try to imitate real life? Like a little girl asking you how old she is if, in ten years, her mom will be twice as old as she will be then? You know, just your everyday conversations and everyday problems. Well, equations are what we use to solve them. Whenever we have some value that we don't know like the age of the little girl , but we know that it must satisfy some property like being twice as large as some other number , we describe this connection using equations. We denote the value we don't know with a symbol, which we call a variable.

Choc chox

In mathematics, solving a matrix and transforming it into RREF is essentially solving a system of linear equations. As soon as it is changed into the reduced row echelon form the use of it in linear algebra is much easier and can be really convenient for mostly mathematicians. These issues are mainly in fund where we need to perform some "choices pricing" or in circulation equation or heat transport. Latest commit History 18 Commits. Result The calculator will immediately process the data and present the Reduced Row Echelon Form of your matrix. Our calculator delivers instantaneous and precise results, which can significantly save your time and reduce potential calculation errors. The site enables users to create a matrix in row echelon form first using row echelon form calculator and then transform it into RREF. It helps simplify the process of solving systems of linear equations. To make our lives easier and simpler actually what mathematics is about , this calculator was created. A matrix in RREF has ones as leading entries in each row, with all other entries in the same column as zeros. Branches Tags.

The calculator will find the row echelon form simple or reduced — RREF of the given augmented if needed matrix, with steps shown. This calculator assists you in solving systems of linear equations by putting a matrix into a row echelon form.

You signed in with another tab or window. Handles Complex Calculations It can handle matrices of different dimensions, allowing for different applications, from simple to more complex systems of equations. This has many use cases in advanced mathematics across several disciplines such as finance and differential equations. In mathematics, solving a matrix and transforming it into RREF is essentially solving a system of linear equations. You switched accounts on another tab or window. All rows of zeros are at the bottom of the matrix. These issues are mainly in fund where we need to perform some "choices pricing" or in circulation equation or heat transport. So in short; these equations are used by Financial Analysts, Quantitative Analysts, and scientists in thermodynamics. Consider the following system of three linear equations:. This has many use cases in advanced mathematics …. Educational Value It not only delivers the solution but also helps you understand the process behind Gauss-Jordan elimination, making it a valuable learning tool. The RREF calculator is used to transform any matrix into the reduced row echelon form. This has many use cases in advanced mathematics … rref-calculator.