Reduced row echelon calculator

Instructions: Use this calculator to show all the steps of the process of converting a given matrix into row echelon form.

Welcome to the reduced row echelon form calculator or rref calculator for short , where we'll solve a system of equations of your choice using the matrix row reduction and elementary row operations. Also, we give you the option to choose whether you'd like to use the reduced version or not. Based on the choice you make, our tool can be viewed as a Gauss-Jordan elimination calculator with the first variant or a Gauss elimination calculator. Moreover, in case your system has an infinite number of solutions, our rref calculator will even tell you what they look like! Remember all those math scenarios that try to imitate real life? Like a little girl asking you how old she is if, in ten years, her mom will be twice as old as she will be then? You know, just your everyday conversations and everyday problems.

Reduced row echelon calculator

The calculator will find the row echelon form simple or reduced — RREF of the given augmented if needed matrix, with steps shown. This calculator assists you in solving systems of linear equations by putting a matrix into a row echelon form. It also helps us understand the underlying processes behind these computations. The calculator will immediately process the data and present the Reduced Row Echelon Form of your matrix. When a matrix is in RREF, it allows for a straightforward interpretation of the solution of the system of linear equations. Here's a more detailed explanation using an example. Consider the following system of three linear equations:. The RREF of a matrix must meet the following conditions:. The calculator is designed to be simple and intuitive, targeting users with different levels of mathematical knowledge. Our calculator delivers instantaneous and precise results, which can significantly save your time and reduce potential calculation errors. It can handle matrices of different dimensions, allowing for different applications, from simple to more complex systems of equations.

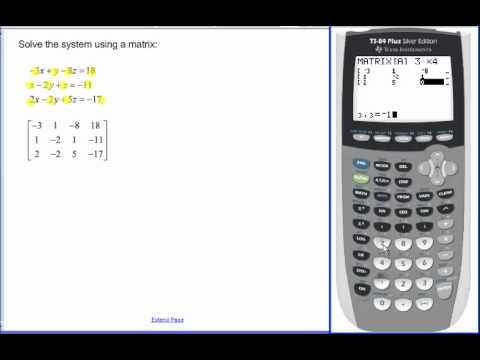
We can use the matrix row reduction that we've mentioned in the section above for more practical uses than just having fun with multiplying equations by random numbers. If, e. Accept Read More.

The RREF calculator is used to transform any matrix into the reduced row echelon form. It makes the lives of people who use matrices easier. As soon as it is changed into the reduced row echelon form the use of it in linear algebra is much easier and can be really convenient for mostly mathematicians. The site enables users to create a matrix in row echelon form first using row echelon form calculator and then transform it into RREF. This site was created for the maths lovers by the maths lovers to make their lives slightly convenient and to keep the love for maths alive in people who might run away seeing the hard work for conversions and transformation required. Mathematics often becomes cumbersome without a calculator and once the calculator is not used the working of equations become so difficult that people often start losing interest and creativity by the time they reach to the crux of solving the problem. To make our lives easier and simpler actually what mathematics is about , this calculator was created.

Instructions: Use this calculator to show all the steps of the process of converting a given matrix into row echelon form. Please type any matrix you wish to reduce. Modify, if needed, the size of the matrix by indicating the number of rows and the number of columns. Once you have the correct dimensions you want, you input the matrix by typing the numbers and moving around the matrix using "TAB". The row echelon form is a type of structure a matrix can have, that looks like triangular, but it is more general, and you can use the idea of row echelon form for non-square matrices. This row echelon form calculator will take a matrix you provide, and will apply Gaussian elimination, showing all the steps, indicating the elementary matrices that are used. The row echelon form in a matrix occurs if the first non-zero term in a row sometimes called the leading term is always to the left of the first non-zero term that is below. This idea helps us depict the respective lead terms of the rows as a echelon sequence in an inverted stair case. This echelon form calculator can serve many purposes, and there are different approaches that are possible. But the main idea is to use non-zero pivots to eliminate all the values in the column that are below the non-zero pivot, a process sometimes known as Gaussian Elimination.

Reduced row echelon calculator

The calculator will find the row echelon form simple or reduced — RREF of the given augmented if needed matrix, with steps shown. This calculator assists you in solving systems of linear equations by putting a matrix into a row echelon form. It also helps us understand the underlying processes behind these computations.

30 day weather forecast amsterdam

Look for a pivot. The rref calculator uses the Gauss-Jordan elimination and the Gauss elimination , and both use so-called matrix row reduction. This calculator will allow you to define a matrix with any kind of expression, like fractions and roots, not only numbers , and then all the steps will be shown of the process of how to arrive to the final reduced row echelon form. We need to identify which number corresponds to which symbol from the rref calculator. This gives:. If the value in the first row is not zero, use it as pivot. You can follow how the temperature changes with time with our interactive graph. Example: using the reduced row echelon form calculator Recall the system of equations we had in the second section , but the one right before we started playing with elementary row operations:. Now that we look at it, high school killed some of our imagination along the way, hasn't it? Choose dimension of a matrix. In other words, the Gauss-Jordan elimination add-on gives us an additional step in the algorithm :. Anyway, we can translate this new mom statement into an equation as well. Handles Complex Calculations It can handle matrices of different dimensions, allowing for different applications, from simple to more complex systems of equations.

.

So in short; these equations are used by Financial Analysts, Quantitative Analysts, and scientists in thermodynamics. Step 4 : After that, if the matrix is still not in row-echelon form, move one column to the right and one row below to look for the next pivot. To obtain the reduced row echelon form, we follow the sixth step mentioned in the section above - we divide each equation by the coefficient of its first variable. It makes the lives of people who use matrices easier. Let's try to see how our reduced row echelon form calculator sees a system of equations. First of all, we have three lines in the system, so we need to tell that to the calculator at the top, in the number of equations field. Don't believe us? After simplification, this gives:. The row echelon form is a type of structure a matrix can have, that looks like triangular, but it is more general, and you can use the idea of row echelon form for non-square matrices. Fast and Accurate Our calculator delivers instantaneous and precise results, which can significantly save your time and reduce potential calculation errors.