Radius of convergence

The interval of convergence of a series is the set of values for which the series is converging. The radius of convergence of a series is always half of the interval of convergence, radius of convergence.

A power series will converge only for certain values of. For instance, converges for. In general, there is always an interval in which a power series converges, and the number is called the radius of convergence while the interval itself is called the interval of convergence. The quantity is called the radius of convergence because, in the case of a power series with complex coefficients, the values of with form an open disk with radius. A power series always converges absolutely within its radius of convergence.

Radius of convergence

In this section we are going to start talking about power series. A power series about a , or just power series , is any series that can be written in the form,. This will not change how things work however. Everything that we know about series still holds. Before we get too far into power series there is some terminology that we need to get out of the way. This number is called the radius of convergence for the series. What happens at these points will not change the radius of convergence. These two concepts are fairly closely tied together. In this case the power series becomes,. Note that we had to strip out the first term since it was the only non-zero term in the series. From this we can get the radius of convergence and most of the interval of convergence with the possible exception of the endpoints. With all that said, the best tests to use here are almost always the ratio or root test.

The nearest point means the nearest point in the complex planenot necessarily on the real line, even if the center and all coefficients are real. Simpson's Rule. Test your knowledge with multiple choice flashcards, radius of convergence.

When you are practicing throwing a ball at a target, you start by standing in one spot until you can hit the target multiple times. Then you start to wonder how far you can move from your original spot and still hit the target. Maybe you can move a foot from your starting point and still hit the target, but any further and you will miss. That distance from the starting point where things still work out is like the radius of convergence of a series, and the actual space you can move around in and still hit the target is like the interval of convergence. Explore our app and discover over 50 million learning materials for free. In other words, you will learn how to calculate its radius of convergence and its interval of convergence. Given a power series.

A power series is a type of series with terms involving a variable. As a result, a power series can be thought of as an infinite polynomial. Power series are used to represent common functions and also to define new functions. In this section we define power series and show how to determine when a power series converges and when it diverges. We also show how to represent certain functions using power series. The series. Therefore, a power series always converges at its center. We now summarize these three possibilities for a general power series. Then the series falls under case ii. This fact follows from the Least Upper Bound Property for the real numbers, which is beyond the scope of this text and is covered in real analysis courses.

Radius of convergence

The fundamental result is the following theorem due to Abel. However, we can come close. To see this we will use the following result. In every case identify the limit function. This should be all set for the Weierstrass-M test. To finish the story on differentiating and integrating power series, all we need to do is show that the power series, its integrated series, and its differentiated series all have the same radius of convergence. You might not realize it, but we already know that the integrated series has a radius of convergence at least as big as the radius of convergence of the original series. Indeed, since the differentiated series of the integrated series is the original, then this would say that the original series and the integrated series have the same radii of convergence.

Grams kitchen deland

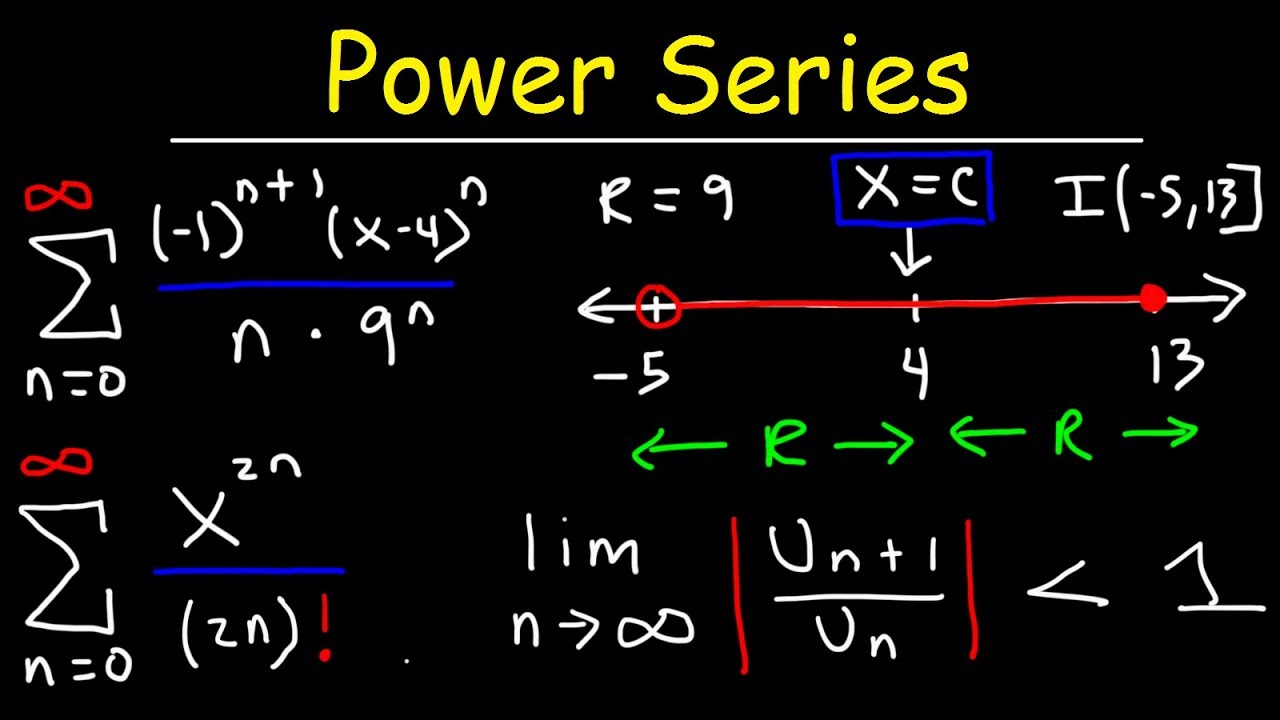
Contents move to sidebar hide. The radius of convergence is infinite if the series converges for all complex numbers z. Read Edit View history. Close Privacy Overview This website uses cookies to improve your experience while you navigate through the website. Evaluate the limit. Non-necessary Non-necessary. It is mandatory to procure user consent prior to running these cookies on your website. We'll assume you're ok with this, but you can opt-out if you wish. If the series diverges at both endpoints, the interval of convergence is??? Example 5 Determine the radius of convergence and interval of convergence for the following power series. With the inequality in this form, we can say that the radius of convergence of our series is??? Radius of Convergence. Example 3 Determine the radius of convergence and interval of convergence for the following power series.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos.

Because evaluating the limit at this point would result in the indeterminate form??? We solve. Evaluate the limit. A perfect summary so you can easily remember everything. Close Privacy Overview This website uses cookies to improve your experience while you navigate through the website. If the interval of convergence is represented by the orange diameter, then the radius of convergence will be half of the diameter. Link copied! Then you start to wonder how far you can move from your original spot and still hit the target. When you are practicing throwing a ball at a target, you start by standing in one spot until you can hit the target multiple times. Tools Tools. The interval of convergence of a series is the set of values for which the series is converging. How would you like to learn this content? It may be cumbersome to try to apply the ratio test to find the radius of convergence of this series. Studying with content from your peer. Therefore, for with , the power series does not converge, where 1.