Quadratic simultaneous equations worksheet
Use this worksheet to revise or practise solving quadratic simultaneous equations at GCSE. Includes an introduction, worked examples, practice questions, extension questions and answers. There are three worked examples to walk students through factorising, rearranging, substituting and simplifying quadratic equations, and using the quadratic formula.
A sequence of lessons I have now successfully delivered to a Year 9 and Year 10 top set and a Year 10 set 2. The students were confident in carrying out the skill of solving quadratic simultaneous equations. I have included plenty of practice questions, some whiteboard questions for AFL, exam type questions and a a difficult challenge question. I have included a bit on solving quadratic simultaneous equation graphically as well. I will upload a worksheet soon to help with teaching this aspect of the topic. Please leave a review if you found this resource useful. Your rating is required to reflect your happiness.
Quadratic simultaneous equations worksheet
Supercharge your learning. Simultaneous equations are multiple equations that share the same variables and which are all true at the same time. When an equation has 2 variables its much harder to solve, however, if you have 2 equations both with 2 variables, like. These equations are called simultaneous for this reason. There are 2 main types of equation you need to be able to solve. We will write one equation on top of the other and draw a line underneath, as with normal subtraction. Example: Find the solution to the following simultaneous equations. The coefficients are the numbers before x and y , make the x coefficients the same by scaling up both equations. Step 3: Add or subtract the equations to eliminate terms with equal coefficients. Step 5: Substitute the answer into the simplest of the two equations to find the other variable. Instead, we have to use substitution. Step 1: Rearrange the linear equation to get one of the unknowns on its own and on one side of the equals sign. Step 2: Substitute the linear equation into the non-linear.
Simultaneous Equations Drill Questions. Still stuck? If we rearrange to make x the subject we find.
We will also discuss their relationship to graphs and how they can be solved graphically. Quadratic simultaneous equations are two or more equations that share variables that are raised to powers up to 2 e. Below are examples of quadratic simultaneous equations that are made up of a pair of equations; one linear equation and one equation with quadratic elements. One key difference of quadratic simultaneous equations is that we can expect multiple answers. This is because of the way the graphs of linear and quadratic or other non-linear functions can intersect.
Quadratic Simultaneous Equations Worksheet. Help your students prepare for their Maths GCSE with this free quadratic simultaneous equations worksheet of 34 questions and answers. To receive this resource and regular emails with more free resources, blog posts and other Third Space updates, enter your email address and click below. You can unsubscribe at any time each email we send will contain an easy way to unsubscribe. To find out more about how we use your data, see our privacy policy. Raise maths attainment across your school with hundreds of flexible and easy to use GCSE maths worksheets and lessons designed by teachers for teachers. Quadratic simultaneous equations are pairs of equations where one is one quadratic and one linear. To solve quadratic simultaneous equations we can use the elimination method in a similar way to solving linear simultaneous equations.
Quadratic simultaneous equations worksheet
We will also discuss their relationship to graphs and how they can be solved graphically. Simultaneous equations are two or more algebraic equations that share variables such as x and y. The number of variables in simultaneous equations must match the number of equations for it to be solved. However when we have at least as many equations as variables we may be able to solve them using methods for solving simultaneous equations. We can consider each equation as a function which, when displayed graphically, may intersect at a specific point. This point of intersection gives the solution to the simultaneous equations.
Sophie arvebrink
Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors. See below:. Find out more about our GCSE maths tuition programme. Empty reply does not make any sense for the end user. If we multiply the second equation by 2 , we have two equations both with a 2A term, hence subtracting our new equation 2 from equation 1 we get,. Username or Email Address. Filter Topic Content Filters. Save for later. Last updated 19 February Share this Share through email Share through twitter Share through linkedin Share through facebook Share through pinterest. These cookies do not store any personal information. One key difference of quadratic simultaneous equations is that we can expect multiple answers. Quadratic simultaneous equations is part of our series of lessons to support revision on simultaneous equations. Then, substituting this value back into the original equation 2 , we get,. Please read our Cookies Policy for information on how we use cookies and how to manage or change your cookie settings.
We will also discuss their relationship to graphs and how they can be solved graphically. Quadratic simultaneous equations are two or more equations that share variables that are raised to powers up to 2 e. Below are examples of quadratic simultaneous equations that are made up of a pair of equations; one linear equation and one equation with quadratic elements.
We will write one equation on top of the other and draw a line underneath, as with normal subtraction. Simultaneous equations are multiple equations that share the same variables and which are all true at the same time. Algebraic fractions When using algebraic fractions to remove the denominator make sure each term is carefully multiplied. Supercharge your learning. Log In. Includes an introduction, worked examples, practice questions, extension questions and answers. If we multiply the first equation by 2 , we have two equations both with a 2y term, hence adding our new equation 1 and equation 2 we get,. Find out more about our GCSE maths tuition programme. Have you used this resource? Get Started. You must be logged in to vote for this question. Graphical representation. Errors can quickly be spotted by substituting your solutions in the original first or second equations to check they work. There are no reviews yet.

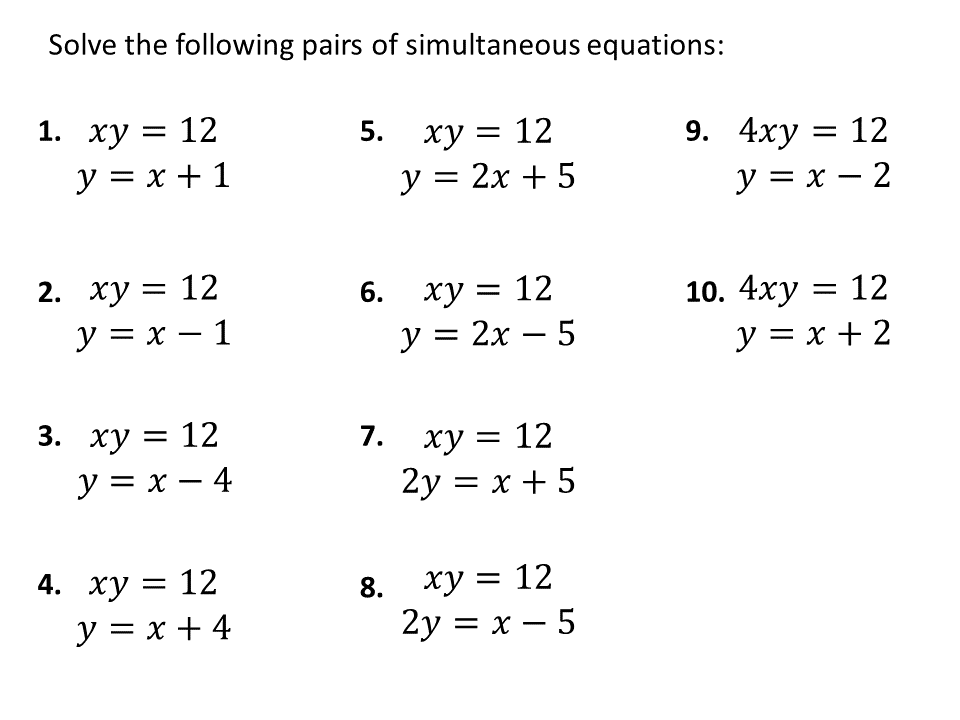
I think, that you commit an error.
Excellent variant
I consider, that you are mistaken. Write to me in PM, we will talk.