N 3 1 4 n
In mathematicsa geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series.
In mathematics, the general root, or the n th root of a number a is another number b that when multiplied by itself n times, equals a. In equation format:. Calculating square roots and n th roots is fairly intensive. It requires estimation and trial and error. There exist more precise and efficient ways to calculate square roots, but below is a method that does not require a significant understanding of more complicated math concepts. Calculating n th roots can be done using a similar method, with modifications to deal with n.
N 3 1 4 n
If it's not what You are looking for type in the equation solver your own equation and let us solve it. Equations solver - equations involving one unknown Quadratic equations solver Percentage Calculator - Step by step Derivative calculator - step by step Graphs of functions Factorization Greatest Common Factor Least Common Multiple System of equations - step by step solver Fractions calculator - step by step Theory in mathematics Roman numerals conversion Tip calculator Numbers as decimals, fractions, percentages More or less than - questions. Toggle navigation GetEasySolution. Check how easy it is, and learn it for the future. Equations solver categories Equations solver - equations involving one unknown Quadratic equations solver Percentage Calculator - Step by step Derivative calculator - step by step Graphs of functions Factorization Greatest Common Factor Least Common Multiple System of equations - step by step solver Fractions calculator - step by step Theory in mathematics Roman numerals conversion Tip calculator Numbers as decimals, fractions, percentages More or less than - questions.
He came up with the answer to the above problem in a matter of seconds. Toggle limited content width. In the theory of Lie groups, the matrix exponential gives the exponential map between a matrix Lie algebra and the corresponding Lie group.
Sum of n terms in a sequence can be evaluated only if we know the type of sequence it is. Usually, we consider arithmetic progression , while calculating the sum of n number of terms. In this progression, the common difference between each succeeding term and each preceding term is constant. An example of AP is natural numbers, where the common difference is 1. Therefore, to find the sum of natural numbers, we need to know the formula to find it. Let us discuss here.
Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here. Each of these series can be calculated through a closed-form formula. Manipulations of these sums yield useful results in areas including string theory , quantum mechanics , and complex numbers.
N 3 1 4 n
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Introduction to arithmetic sequences. Get comfortable with the basics of explicit and recursive formulas for arithmetic sequences. Before taking this lesson, make sure you know the basics of arithmetic sequences and have some experience with evaluating functions and function domain.
We fut
In mathematics , the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. Main article: Single-precision floating-point format. In the study of fractals , geometric series often arise as the perimeter , area , or volume of a self-similar figure. List Of All Prime Numbers. These "generalized binomial coefficients" appear in Newton's generalized binomial theorem. The resulting numbers are called multiset coefficients ; [18] the number of ways to "multichoose" i. Categories : Geometric series Ratios. This can be proved by induction using 3 or by Zeckendorf's representation. Categories : Combinatorics Factorial and binomial topics Integer sequences Triangles of numbers Operations on numbers. In contrast, the complex geometric series has all the terms rotating in the same direction and it can trace only circles. Calculus with Analytic Geometry , 8th ed. The bivariate generating function of the binomial coefficients is. Alternative notations include C n , k , n C k , n C k , C k n , [3] C n k , and C n , k , in all of which the C stands for combinations or choices. The resulting function has been little-studied, apparently first being graphed in Fowler Fractional Malliavin Stochastic Variations.
We have seen that the integral test allows us to determine the convergence or divergence of a series by comparing it to a related improper integral. In this section, we show how to use comparison tests to determine the convergence or divergence of a series by comparing it to a series whose convergence or divergence is known. Typically these tests are used to determine convergence of series that are similar to geometric series or p-series.
It can be simplified as:. As is, the Elements of Geometry is over pages of propositions and proofs. For finite cardinals, this definition coincides with the standard definition of the binomial coefficient. Thomas 18 July Calculus on Euclidean space Generalized functions Limit of distributions. Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem. Binomial transform Delannoy number Eulerian number Hypergeometric function List of factorial and binomial topics Macaulay representation of an integer Motzkin number Multiplicities of entries in Pascal's triangle Narayana number Star of David theorem Sun's curious identity Table of Newtonian series Trinomial expansion. A related combinatorial problem is to count multisets of prescribed size with elements drawn from a given set, that is, to count the number of ways to select a certain number of elements from a given set with the possibility of selecting the same element repeatedly. This is the difference of two geometric series, and so it is a straightforward application of the formula for infinite geometric series that completes the proof. Guess: 1. The left and right sides are two ways to count the same collection of subsets, so they are equal. Guess: 5.

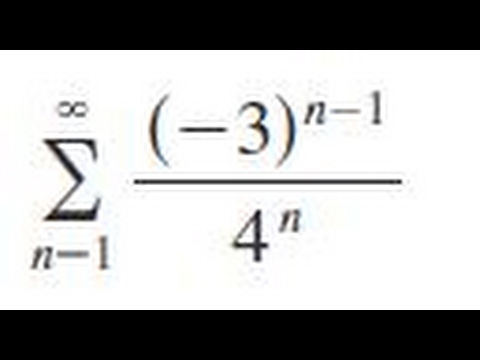
Excuse, the question is removed
It is a pity, that now I can not express - it is very occupied. I will return - I will necessarily express the opinion on this question.
I apologise, but, in my opinion, you are mistaken. I suggest it to discuss. Write to me in PM, we will talk.