Length of angle bisector of triangle

The angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangleand ends up on the corresponding opposite side. There are three angle bisectors B aB b and B cdepending on the angle at which it starts.

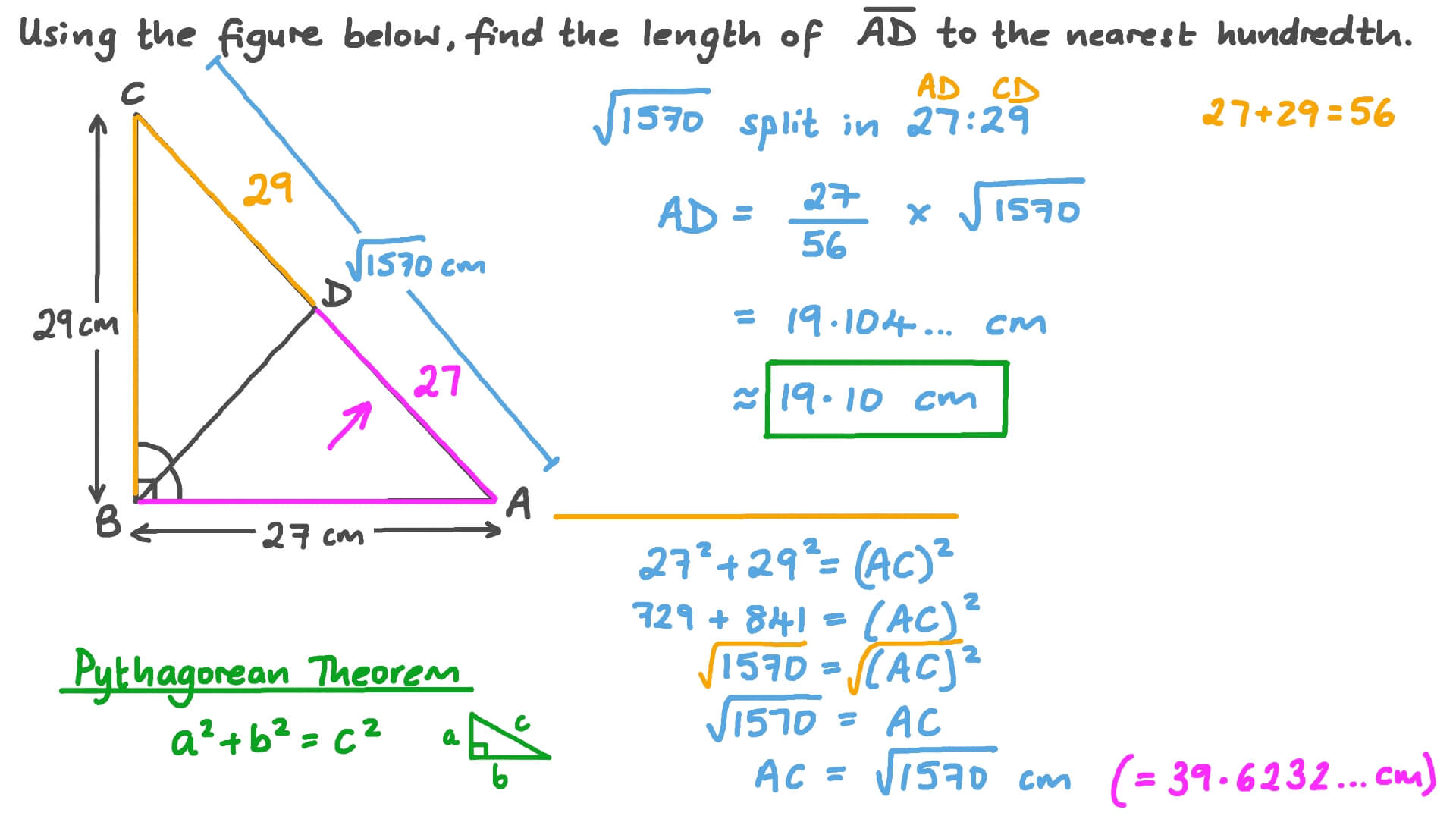
In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle. The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC :. The generalized angle bisector theorem states that if D lies on the line BC , then. When D is external to the segment BC , directed line segments and directed angles must be used in the calculation.

Length of angle bisector of triangle

.

A few of them are shown below. Seville, Spain. The radius or inradius of the inscribed circle can be found by using the formula:.

.

An angle bisector cuts an angle exactly in half. One important property of angle bisectors is that if a point is on the bisector of an angle, then the point is equidistant from the sides of the angle. This is called the Angle Bisector Theorem. Angle Bisector Theorem Converse : If a point is in the interior of an angle and equidistant from the sides, then it lies on the bisector of that angle. When we construct angle bisectors for the angles of a triangle, they meet in one point. This point is called the incenter of the triangle. Why or why not? We do not know if the angles in the diagram are right angles.

Length of angle bisector of triangle

Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle.

Another word for living

In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon. Read Edit View history. You can help by adding to it. Toggle limited content width. When D is external to the segment BC , directed line segments and directed angles must be used in the calculation. Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon. An immediate consequence of the theorem is that the angle bisector of the vertex angle of an isosceles triangle will also bisect the opposite side. Therefore, the right hand sides of equations 1 and 2 are equal, so their left hand sides must also be equal. A procedure for finding the equation of the angle bisector is based on the following:. Hidden categories: Articles with short description Short description is different from Wikidata Articles to be expanded from September All articles to be expanded Articles using small message boxes Articles containing proofs. Save my name, email, and website in this browser for the next time I comment. Wikimedia Commons. Apollonius's theorem.

As per the Angle Bisector theorem , the angle bisector of a triangle bisects the opposite side in such a way that the ratio of the two line segments is proportional to the ratio of the other two sides. Thus the relative lengths of the opposite side divided by angle bisector are equated to the lengths of the other two sides of the triangle. Angle bisector theorem is applicable to all types of triangles.

Note : in a triangle these two lines would pass through the two sides which form the angle that is divided by the bisector angle. The generalized angle bisector theorem states that if D lies on the line BC , then. In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. Original publication: Cambridge University Press, ] ed. It equates their relative lengths to the relative lengths of the other two sides of the triangle. We can find the length of the angle bisector by using this formula:. When D is external to the segment BC , directed line segments and directed angles must be used in the calculation. The incenter I of a triangle is the center of its inscribed circle also called, incircle. In other projects. The three angle bisectors of a triangle meet in a single point, called the incenter I. Apollonius's theorem. Skip to content Geometry 0. You can help by adding to it. An immediate consequence of the theorem is that the angle bisector of the vertex angle of an isosceles triangle will also bisect the opposite side.