Laplace transform of unit step function
If you're seeing this message, it means we're having trouble loading external resources on our website.
To productively use the Laplace Transform, we need to be able to transform functions from the time domain to the Laplace domain. We can do this by applying the definition of the Laplace Transform. Our goal is to avoid having to evaluate the integral by finding the Laplace Transform of many useful functions and compiling them in a table. Thereafter the Laplace Transform of functions can almost always be looked by using the tables without any need to integrate. A table of Laplace Transform of functions is available here. In this case we say that the "region of convergence" of the Laplace Transform is the right half of the s-plane since s is a complex number, the right half of the plane corresponds to the real part of s being positive. As long as the functions we are working with have at least part of their region of convergence in common which will be true in the types of problems we consider , the region of convergence holds no particular interest for us.
Laplace transform of unit step function
Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t. The switching process can be described mathematically by the function called the Unit Step Function otherwise known as the Heaviside function after Oliver Heaviside. That is, u is a function of time t , and u has value zero when time is negative before we flip the switch ; and value one when time is positive from when we flip the switch. In this work, it doesn't make a great deal of difference to our calculations, so we'll continue to use the first interpretation, and draw our graphs accordingly. Such a function may be described using the shifted aka delayed unit step function. We write such a situation using unit step functions as:. Write the following functions in terms of unit step function s. Sketch each waveform.
Transform of Periodic Functions 6. The unit impulse is discussed elsewherebut to review. Yes, Heaviside function
Online Calculus Solver ». IntMath f orum ». We saw some of the following properties in the Table of Laplace Transforms. We write the function using the rectangular pulse formula. We also use the linearity property since there are 2 items in our function.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Properties of the Laplace transform. About About this video Transcript. Introduction to the unit step function and its Laplace Transform. Created by Sal Khan. Want to join the conversation?
Laplace transform of unit step function
Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t. The switching process can be described mathematically by the function called the Unit Step Function otherwise known as the Heaviside function after Oliver Heaviside. That is, u is a function of time t , and u has value zero when time is negative before we flip the switch ; and value one when time is positive from when we flip the switch.
Mentone homes for sale
It might have, continued and done something crazy, but what we did is we shifted it from here to there, and then we zeroed out everything before c. In fact, at this point, this unit step function, it has no use anymore. Example: Laplace Transform of a Gated Sine Find the Laplace Transform of the function shown: Solution : This function is a little different than the previous in that it involves more than ramps and steps. Because we saw, in our definition of the Laplace transform, we're always taking the integral from 0 to infinity, so we're only dealing with the positive x-axis. Let's say it goes to zero until-- I don't know, I'll call that c again. Comment Button navigates to signup page. And then the other thing I said is that the unit step function, it's going to be 1 over this entire range of potential t-values, so we can just kind of ignore it. I hope this helps someone. Show preview Show formatting options Post answer. Transform of Unit Step Functions 5. This thing is really malfunctioning at this point right here. Disclaimer: IntMath. Until we get to c, the unit step function is zero when it's less than c. Aviv 'Shual' Eshed. And then we'll call this f of t.
Online Calculus Solver ». IntMath f orum ».
If you create a function by multiplying two functions in time, there is no easy way to find the Laplace Transform of the resulting function. Oliver Heaviside 1b. When composing a complex function from elementary functions, it is important to only use addition. So let's say that just my regular f of t-- let me, this is x. But I said that we have to also-- if I just shifted this function, you would have all this other stuff, because you would have had all this other stuff when the function was back here still going on. I hope this clears it up a bit for you, let me know if you have any more questions. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t. And I'll do a little thicker line. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. So how can we construct this yellow function, where it's essentially a shifted version of this green function, but it's zero below c? So if we want to essentially find the area under this curve, we can ignore all the stuff that happens before c. Let me draw my x-axis right here. And we know what the Laplace transform of sine of t is. Thereafter the Laplace Transform of functions can almost always be looked by using the tables without any need to integrate. So it has to be 2 minus 2, so I'll have to put at 2 here, and this should work.

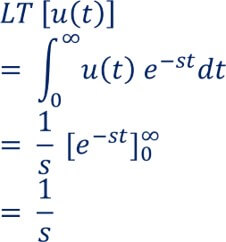
I apologise, but, in my opinion, you commit an error. Let's discuss it. Write to me in PM, we will talk.