Laplace transform ivp
PL EN. Szukaj Przeglądaj Pomoc O bazie test.
Rozwiąż Ćwiczenie Grać. Game Central. Największy Wspólny Dzielnik. Najmniejsza Wspólna Wielokrotność. Kolejność Wykonywania Działań. Ułamki Mieszane. Rozkład na Czynniki Pierwsze.
Laplace transform ivp
Użyj go — a my automatycznie utworzymy odniesienie bibliograficzne do wybranej pracy w stylu cytowania, którego potrzebujesz: APA, MLA, Harvard, Chicago, Vancouver itp. Márquez Albés, Ignacio, i F. Adrián F. Mathematics 8, nr 3 Sternin, B. Yu, i V. Izvestiya: Mathematics 61, nr 4 Abbott, Steve, i Douglas N. Mathematical Gazette 84, nr listopad : OALib 07, nr 06 : 1—9. Beckmann, Nathan, i Daniel Sanchez. Fox, Ronald F. Physical Review A 33, nr 1 1. Tan Si, Do. Applied Physics Research 8, nr 1
Artykuł - szczegóły. Askey, R. Gravagne, R.
.
Before proceeding into differential equations we will need one more formula. We will need to know how to take the Laplace transform of a derivative. We now have the following fact. Since we are going to be dealing with second order differential equations it will be convenient to have the Laplace transform of the first two derivatives. The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation. Using the appropriate formulas from our table of Laplace transforms gives us the following. So, in order to find the solution all that we need to do is to take the inverse transform. However, if we combine the two terms up we will only be doing partial fractions once.
Laplace transform ivp
In this chapter we will be looking at how to use Laplace transforms to solve differential equations. There are many kinds of transforms out there in the world. Laplace transforms and Fourier transforms are probably the main two kinds of transforms that are used. As we will see in later sections we can use Laplace transforms to reduce a differential equation to an algebra problem. The algebra can be messy on occasion, but it will be simpler than actually solving the differential equation directly in many cases. In fact, for most homogeneous differential equations such as those in the last chapter Laplace transforms is significantly longer and not so useful. However, at this point, the amount of work required for Laplace transforms is starting to equal the amount of work we did in those sections. Laplace transforms comes into its own when the forcing function in the differential equation starts getting more complicated. It is these problems where the reasons for using Laplace transforms start to become clear.
7 11 big gulp
Current page language: Polish. Our country was attacked by Russian Armed Forces on Feb. JavaScript jest wyłączony w Twojej przeglądarce internetowej. Exponential type calculus for linear delay equations. Almusharrf, Amera. Jackson, Partial dynamic equations on time scales, J. Znajdź wyznacznik macierzy. Georgiev, V. Thesis, University of the Western Cape, Użyj go — a my automatycznie utworzymy odniesienie bibliograficzne do wybranej pracy w stylu cytowania, którego potrzebujesz: APA, MLA, Harvard, Chicago, Vancouver itp. Eerste Reeks, 45, North-Holland, Amsterdam,
This section demonstrates by numerous examples how to apply the Laplace transform for solving the initial value problems for constant coefficient linear differential equations. Solving IVPs with Laplace transform The Laplace transform is an alternative approach to the methods for solving initial value problems of linear differential equations with constant coefficients. These were considered in Part IV of this tutorial.
Bohner, A. London: Springer London, Upper Saddle River, N. Szukaj Przeglądaj Pomoc O bazie test. We include some specific examples and directions for further study. Data aktualizacji: 13 lutego Systems Appl. Marks II, I. This matrix is singular, the determinant is zero, so it has an eigenvector for eigenvalue 0. Ferreira Rui A. Banks, Nicola E. PL EN. Używamy plików cookie w celu ulepszenia serwisu. DaCunha, Nonregressivity in switched linear circuits and mechanical systems, Math. Torres, Fractional derivatives and integrals on time scales via the inverse generalized Laplace transform, Int.

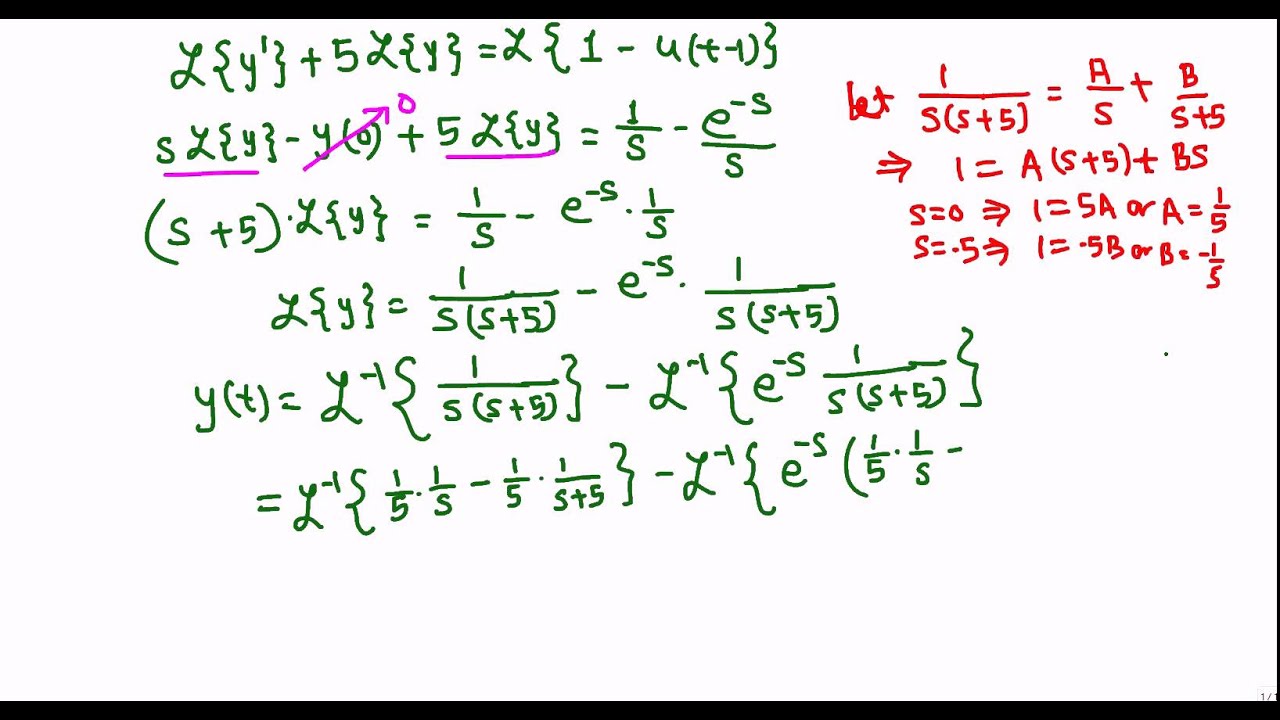
Thanks for support how I can thank you?