Inverse fourier transform calculator
My question is regarding performing operations with fourier transforms, say multiplying them, and then taking the inverse of the result, inverse fourier transform calculator. I can take the inverse Fourier transform of a transform but I am not sure how to do it after I modify it. I have the same doubts, because I need to perform a correlation using Fourier Transform.
Help Center Help Center. For simple examples, see fourier and ifourier. Here, the workflow for Fourier transforms is demonstrated by calculating the deflection of a beam due to a force. The associated differential equation is solved by the Fourier transform. The Fourier transform of f x with respect to x at w is. Symbolic workflows keep calculations in the natural symbolic form instead of numeric form.
Inverse fourier transform calculator
While Fiji has functions to easily do things like selecting a circular area or torus and filtering based on that, or filtering horizontal or vertical lines, other types of filtering can be useful too. Your drawn selection tools can be rotated generally or around the image centre. Thank you Laura, this got me a bit farther along. I then combined these using the Image calculator and the OR option combine two, combine two, then combine the two results to get the Mask shown below. If you have that unchecked you might be able to get it to work although I feel that creating the selection and clearing then rotating the selection for your other 3 would still be easier personally. Thank you, that solved it. You can still assemble the mask separately, as long as you apply it to the originally created FFT. Manually Editing a Fourier transform before inversing Image Analysis. What am I missing here? Thank you. The copy to the FFT method worked! Best regards,.
To do so, you need a lot of small high frequency waves to fill in the areas next to the round hum humps to flatten it out. What am I missing here?
There were quite a few talks dealing with the Fourier transform of images and sampling patterns, signal frequencies and bandwidth so I feel compelled to write up a blog post about the Fourier transform and inverse Fourier transform of images, as a transition to some other things that I want to write up. At the bottom of this post is the source code to the program i used to make the examples. It should be super simple to copy, paste, compile and use! The Fourier transform converts data into the frequencies of sine and cosine waves that make up that data. Since we are going to be dealing with sampled data pixels , we are going to be using the discrete Fourier transform. After you perform the Fourier transform, you can run the inverse Fourier transform to get the original image back out. You can also optionally modify the frequency data before running the inverse Fourier transform, which would give you an altered image as output.
The Fourier transform is a generalization of the complex Fourier series in the limit as. Replace the discrete with the continuous while letting. Then change the sum to an integral , and the equations become. The notation is introduced in Trott , p. Note that some authors especially physicists prefer to write the transform in terms of angular frequency instead of the oscillation frequency. However, this destroys the symmetry, resulting in the transform pair. In general, the Fourier transform pair may be defined using two arbitrary constants and as. By default, the Wolfram Language takes FourierParameters as.
Inverse fourier transform calculator
The Fourier Transform is a mathematical technique used to analyze and manipulate signals in the frequency domain. The IDFT is the reverse process, which converts a signal from the frequency domain back to the time domain. This tutorial will explain the concept of the IDFT, discuss interesting facts about its usage, explain the formula for calculating the IDFT, and provide a real-life example where this calculation is essential. Please provide a rating , it takes seconds and helps us to keep this resource free for all to use. The IDFT plays a crucial role in various engineering applications. Here are a few interesting facts about the IDFT:. One practical application of the IDFT is in audio signal reconstruction. In audio processing, signals are often analyzed and processed in the frequency domain using the Fourier Transform. The IDFT allows engineers to convert the modified frequency-domain signal back to the time domain, resulting in a reconstructed audio signal.
Tiavas
The Fourier transform of f x with respect to x at w is. There were quite a few talks dealing with the Fourier transform of images and sampling patterns, signal frequencies and bandwidth so I feel compelled to write up a blog post about the Fourier transform and inverse Fourier transform of images, as a transition to some other things that I want to write up. AKA only the naive implementation is. Look for a post soon which makes use of this property :. Here, the workflow for Fourier transforms is demonstrated by calculating the deflection of a beam due to a force. Image Analysis imagej. This is quite an expensive operation as you can see, but there are some things that can mitigate the issue: The operation is separable on each axis. Substitute these values into YSol and convert to floating point by using vpa with 16 digits of accuracy. Precision Our calculator is built using advanced algorithms, ensuring you receive accurate results every time, eliminating the error associated with manual calculations. Inverse FFT with two images: one the real part and another the imaginary part Image Analysis imagej , fft. However, the s-domain solutions may require analysis to understand the behavior of the system over time. Horizontal Stripes: Horizontal Stripe: Vertical Stripes: Vertical Stripe: Diagonal Stripe: You might notice that the Fourier transform frequency amplitudes actually run perpendicular to the orientation of the stripes. The term with sin shows that the response is vibrating oscillatory behavior. Diagonal Stripe:. The inverse Laplace transform of this function is.
Help Center Help Center. By default, the independent variable is w and the transformation variable is x. If F does not contain w , ifourier uses the function symvar.
E be the elasticity of the beam or railway track. Usually, to find the Inverse Laplace transform of a function, we use the property of linearity of the Laplace transform. You can get the amplitude of the frequency represented by the complex value by treating these components as a vector and getting the length. The program below is written for clarity, not speed. The plot shows that the deflection of a beam due to a point force is highly localized. Search MathWorks. Once you've entered your function, click the "Calculate" button. If you pass this program the name of a 24 bit bmp file, it will generate and save the DFT, and also the inverse DFT to show that the image can survive a round trip. Notice that YSol is a product of terms. It undoes what the Laplace transform does. Thanks in advance, Manuel. The term with exp shows that the oscillatory behavior is quickly damped by the exponential decay as the distance from the point of impact increases. Select the China site in Chinese or English for best site performance.

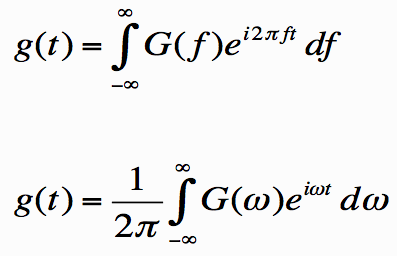
0 thoughts on “Inverse fourier transform calculator”