If a tangent of slope 2 of the ellipse
S K Goyal. Learn from their 1-to-1 discussion with Filo tutors. Total classes on Filo by this tutor - 5, Teaches : Mathematics, Physical Chemistry, Physics.
Formula and problems based on the concept of the equation of tangents to the ellipse. In the plane, a curve surrounds the two focal points so that the distances to the focal points are constant at all points on the curve. Circles are thought to be special types of ellipses that have their points of focus in the same place. Lines crossing each other at a point on an ellipse are known as tangents. The equation of the chord to the ellipse. Let P x1, y1 and Q x2, y2 be two points on the ellipse. The equation of the line PQ is,.
If a tangent of slope 2 of the ellipse
S K Goyal. Learn from their 1-to-1 discussion with Filo tutors. Total classes on Filo by this tutor - 5, Teaches : Mathematics, Physical Chemistry, Physics. Views: 5, Views: 6, Connect with our Mathematics tutors online and get step by step solution of this question. Are you ready to take control of your learning? Chapter 1: Coordinate System and Coordinates questions. Chapter 2: The Straight Lines questions. Chapter 3: Pair of Straight Lines questions. Chapter 4: Circle questions. Chapter 5: Parabola questions. Chapter 6: Ellipse questions. Chapter 7: Hyperbola questions.
The equation of the line PQ is. Zero Vector A zero vector is defined as a line segment coincident with its beginning and ending points. Views: 5,
.
In math we study a term known as tangent in different scenarios. In Euclidean Geometry, tangent to a curve is a straight line that touches a curve once at a single point and does not cut that curve. In Analytic Geometry such tangents drawn to a circle, ellipse , parabola or any arbitrary curve can be described by equations and used to solve various geometric problems. In differential calculus, a tangent to the graph of a function at a point helps us find the rate of change of the function at that point. The tangent of an angle in trigonometry is defined using the eagles and sides of a right angled triangle and has various applications in trigonometry. Let us study about tangents in detail. In geometry, the tangent to a plane curve at a given point is the straight line that just touches the curve at that point. In other words, it does not cut or intersects the curve, it just touches it. In the above image the green line indicates a tangent as it touches the red colored curve at just one point. We should see that the tangent does not cut or intersect the curves.
If a tangent of slope 2 of the ellipse
An ellipse is a curve in the plane which surrounds the two focal points such that the distances to the focal point remain constant for each point on the curve. A circle is said to be a special type of ellipse having both focal points at the same point. A line which intersects the ellipse at a point is called a tangent to the ellipse. The different forms of the tangent equation are given below:. Put your understanding of this concept to test by answering a few MCQs. Your Mobile number and Email id will not be published. Post My Comment. Definitions of an Ellipse. Visualising Ellipses.
60grocery
Chapter 4: Circle questions. Talk to a tutor now students are taking LIVE classes. These are the equations of a tangent to an ellipse. Chapter 2: The Straight Lines questions. The foci are always on major axes. Advanced Problems in Mathem Learn Practice Revision Succeed. Calculus: Early Transcenden Download Filo and start learning with your favourite tutors right away! Instant help, 24x7. Ravi Prakash.
Browsing through Google searches about tangents to an ellipse, I found an equation that I had never seen before, and none of the sites mention how to prove this relationship. Determined to find the proof, I finally found it, and it was not at all hard. I will go through the proof of the equation of a tangent to an ellipse, while noting some properties.
Question 4. Stuck on the question or explanation? Topic: Mathematics. Question 4. Essay review. Equation of a tangent to the ellipse problems 1. As shown above, the various tangent lines of an ellipse can be expressed as follows:. Schedule classes. Eliminating y between 4 and 5 , we get;. Point of intersection of two tangents at points Since we are given the points, we can find the equation of both the tangents using a formula for the equation of tangent in point form.

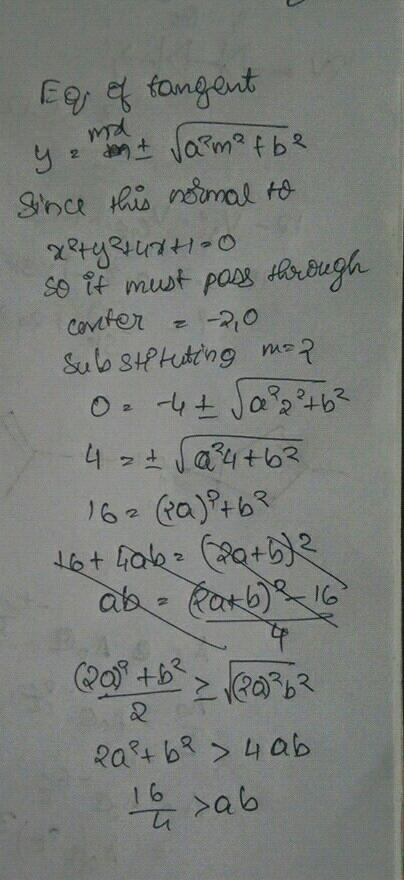
In my opinion you commit an error. Write to me in PM.