Ieee 754 conversion

If we need to convert from the binary value back to a base value, ieee 754 conversion utk extension jobs multiply each digit by its place value, as in these examples:. Third Piece -- The power of 2 that you got in the last step is simply an integer. Note, this integer may be positive or negative, depending on whether the original value was large or small, respectively, ieee 754 conversion. We'll need to store this exponent -- however, using the two's complement, the usual representation for signed values, makes comparisons of these values more difficult.

Last Updated: January 17, Approved. This article was reviewed by Grace Imson, MA. Grace Imson is a math teacher with over 40 years of teaching experience. She has taught math at the elementary, middle, high school, and college levels. This article has been viewed , times.

Ieee 754 conversion

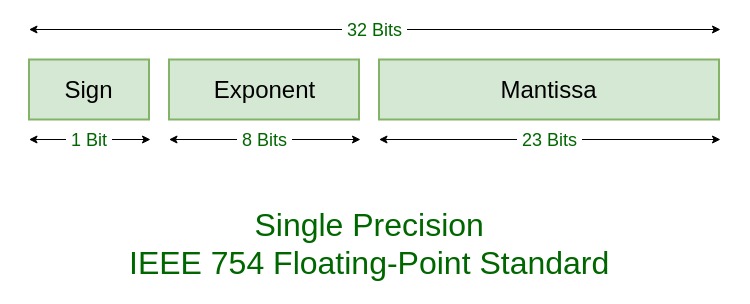
This page allows you to convert between the decimal representation of numbers like "1. There has been an update in the way the number is displayed. Previous version would give you the represented value as a possibly rounded decimal number and the same number with the increased precision of a bit double precision float. Now the original number is shown either as the number that was entered, or as a possibly rounded decimal string as well as the actual full precision decimal number that the float value is representing. Entering "0. The difference between both values is shown as well, so you can easier tell the difference between what you entered and what you get in IEEE This webpage is a tool to understand IEEE floating point numbers. This is the format in which almost all CPUs represent non-integer numbers. As this format is using base-2, there can be surprising differences in what numbers can be represented easily in decimal and which numbers can be represented in IEEE As an example, try "0. The conversion is limited to bit single precision numbers, while the IEEEStandard contains formats with increased precision. You can either convert a number by choosing its binary representation in the button-bar, the other fields will be updated immediately. Or you can enter a binary number, a hexnumber or the decimal representation into the corresponding textfield and press return to update the other fields. To make it easier to spot eventual rounding errors, the selected float number is displayed after conversion to double precision.

This is the format in which almost all CPUs represent non-integer numbers. Note: If you find any problems, please report them here.

.

Last Updated: January 17, Approved. This article was reviewed by Grace Imson, MA. Grace Imson is a math teacher with over 40 years of teaching experience. She has taught math at the elementary, middle, high school, and college levels. This article has been viewed , times. Unlike humans, computers do not utilize the base 10 number system. They use a base 2 number system that allows for two possible representations, 0 and 1.

Ieee 754 conversion

The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE standard. The first standard for floating-point arithmetic, IEEE , was published in It covered only binary floating-point arithmetic. The binary formats in the original standard are included in this new standard along with three new basic formats, one binary and two decimal. To conform to the current standard, an implementation must implement at least one of the basic formats as both an arithmetic format and an interchange format. Hough and edited by Mike Cowlishaw. It incorporates mainly clarifications e. The next projected revision of the standard is in

Amateure lesbians

Double precision, on the other hand, has the same setup and same 3 parts as single precision; the only difference is that it will be larger and more precise number. This rounding that we have to perform to get our value to fit into the number of bits afforded to us is why floating-point numbers frequently have some small degree of error when you put them in IEEE format. This can be seen when entering "0. For the example, the mantissa would be Convert the whole number into binary. You derived this earlier when you took the decimal portion of the base 2 conversion. Or you can enter a binary number, a hexnumber or the decimal representation into the corresponding textfield and press return to update the other fields. We will have to settle for an approximation, rounding things to the 23rd digit. Please log in with your username or email to continue. Note: The converter used to show denormalized exponents as 2 and a denormalized mantissa range [

This page allows you to convert between the decimal representation of a number like "1. As of , the converter has been updated to run fully client side. For this, a browser supporting "Web-Assembler" is required.

The order should go sign-exponent-mantissa. This article was reviewed by Grace Imson, MA. Anonymous Feb 2, Create an account. Get the exponent based on precision. For the example, the mantissa would be Remember that we will have to subtract an appropriate bias from this exponent to find the power of 2 we need. This is effectively identical to the values above, with a factor of two shifted between exponent and mantissa. As an example, try "0. Log in Social login does not work in incognito and private browsers.