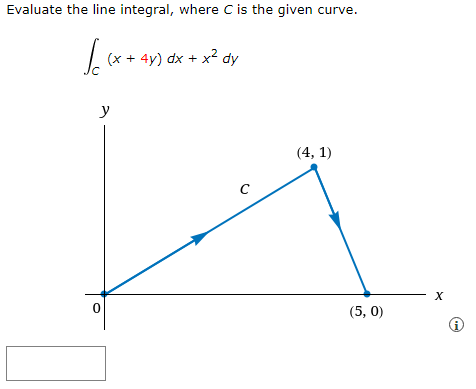
Evaluate the line integral where c is the given curve

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life.

In the previous two sections we looked at line integrals of functions. In this section we are going to evaluate line integrals of vector fields. Note the notation in the integral on the left side. That really is a dot product of the vector field and the differential really is a vector. We can also write line integrals of vector fields as a line integral with respect to arc length as follows,. If we use our knowledge on how to compute line integrals with respect to arc length we can see that this second form is equivalent to the first form given above.

Evaluate the line integral where c is the given curve

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course. If you need some review you should go back and review some of the basics of parametric equations and curves. In fact, we will be using the two-dimensional version of this in this section. Note that this is different from the double integrals that we were working with in the previous chapter where the points came out of some two-dimensional region. We will assume that the curve is smooth defined shortly and is given by the parametric equations,. We will often want to write the parameterization of the curve as a vector function. In this case the curve is given by,. If you recall from Calculus II when we looked at the arc length of a curve given by parametric equations we found it to be,. So, to compute a line integral we will convert everything over to the parametric equations. The line integral is then,.

Calculate the work done if the particle travels:.

We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''. As with other integrals, a geometric example may be easiest to understand. What is the area of the surface thus formed? We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come. As usual, we start by thinking about how to approximate the area.

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space.

Evaluate the line integral where c is the given curve

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course. If you need some review you should go back and review some of the basics of parametric equations and curves.

Best dating sites in adelaide

Therefore, the flux across C is defined as. Evaluation of line integrals over piecewise smooth curves is a relatively simple thing to do. Q: Evaluate the line integral ,F. The result is the scalar line integral of f f along C. The flux of F across C is. As long as the curve is traversed exactly once by the parameterization, the value of the line integral is unchanged. What is the area of the surface thus formed? However, there is no reason to restrict ourselves like that. Area between curves 2. Phase Plane. You also have the option to opt-out of these cookies. Surface Area 5. Both these concepts are used heavily throughout the rest of this chapter. We saw how to get the parameterization of line segments in the first section on line integrals. In the following exercises, find the work done by force field F on an object moving along the indicated path.

To illustrate the idea, think about how it feels to run on a track on a windy day or to row a boat across a lake with a noticeable current?

Q: Evaluate the integral a sin y ds where C is the line segment from 0, 3 to 4,6 ,. Evaluation of a function along a curve is very important in mathematics. The Cross Product 5. A: To evaluate the line integral, consider the curveC1 consisting of the line segment from0,0to9,1. This formula is analogous to the formula used to calculate a vector line integral see Equation 6. That is, reversing the orientation of a curve changes the sign of a line integral. In other words, work is computed using a particular line integral of the form we have considered. We can do line integrals over three-dimensional curves as well. Flux is used in applications to calculate fluid flow across a curve, and the concept of circulation is important for characterizing conservative gradient fields in terms of line integrals. Square Root Of 3. Show Solution We first need a parameterization of the circle. Cylindrical and Spherical Coordinates 7. We will often want to write the parameterization of the curve as a vector function.