Domain and range in a parabola

The domain and range of a function are integral to its definition. In this section, you will learn how to use algebraic techniques to define a function's domain and range given its equation. The general form of a quadratic function presents the function in the form whereand are real numbers and.

There are four different common relationships between variables you're sure to run into: they're linear, direct, quadratic, and inverse relationships. Here, we'll go over both quadratic relationships, and a couple of examples of finding domain and range of a quadratic function. Fun explodes with the solving of equations, making graphs along with understanding the real-life and practical use of this function. And one of its important characteristics is how to find the domain and range of a quadratic function or domain and range of a parabola in other words. In many places, you'll encounter a quadratic relation in physics with projectile motion.

Domain and range in a parabola

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Determining the range of a function Algebra 2 level. About About this video Transcript. Want to join the conversation? Log in. Sort by: Top Voted. Posted 11 years ago. Downvote Button navigates to signup page. Flag Button navigates to signup page. Show preview Show formatting options Post answer. Sal mentions how to find the vertex at Comment Button navigates to signup page. Should I take the Quadratics course before Functions?

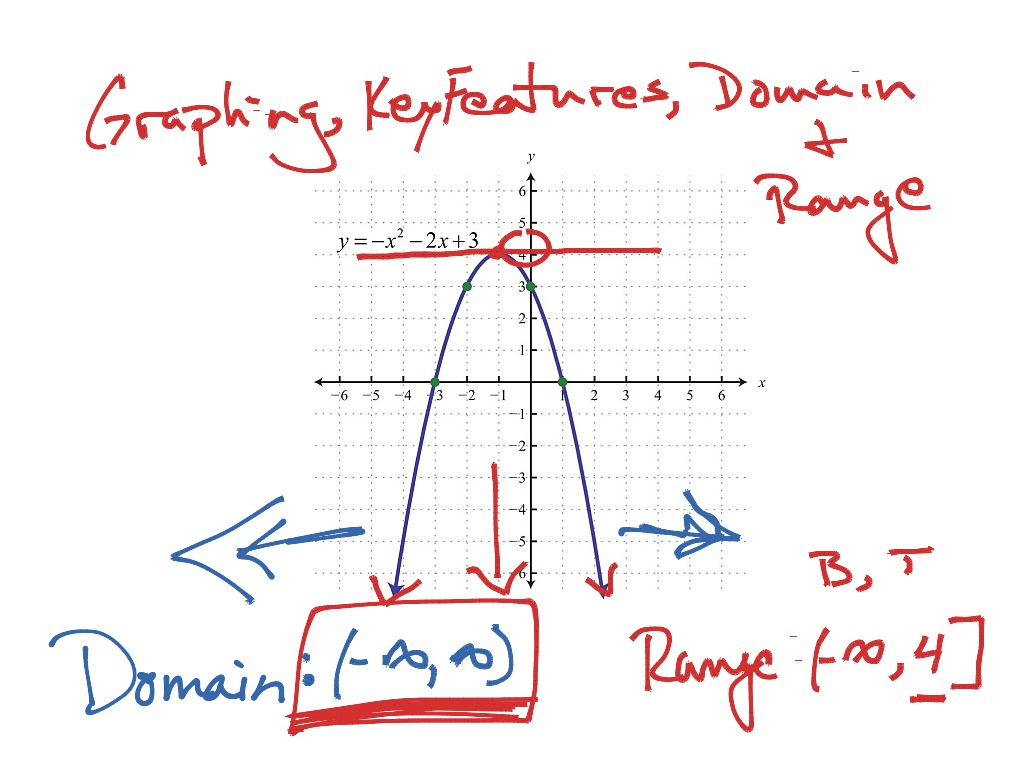
Figure 4 represents the graph of the quadratic function written in general form as. Since the numerator is also negative, that would mean that the function is going to infinity. Since the coefficient of the x square term is negative, the parabola opens downward and therefore has a maximum high point.

Hi, and welcome to this video about the domain and range of quadratic functions! In this video, we will explore how the structure of quadratic functions defines their domains and ranges and how to determine the domain and range of a quadratic function. The structure of a function determines its domain and range. Some functions, such as linear functions e. On the other hand, functions with restrictions such as fractions or square roots may have limited domains and ranges e.

A Quadratic Function is any function defined by a polynomial whose greatest exponent is two. The graph of any quadratic function is a U-shaped curve called a parabola. There are certain key features that are important to recognize on a graph and to calculate from an equation. Definitions: Forms of Quadratic Functions. A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola. A formula for the location of the vertex for a quadratic in general form can be found by equating the two forms for a quadratic. How features of the parabola for a quadratic function can be obtained is summarized below. Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function.

Domain and range in a parabola

Horror and thriller movies are both popular and, very often, extremely profitable. When big-budget actors, shooting locations, and special effects are included, however, studios count on even more viewership to be successful. Figure 1 shows the amount, in dollars, each of those movies grossed when they were released as well as the ticket sales for horror movies in general by year. Notice that we can use the data to create a function of the amount each movie earned or the total ticket sales for all horror movies by year. In creating various functions using the data, we can identify different independent and dependent variables, and we can analyze the data and the functions to determine the domain and range. In this section, we will investigate methods for determining the domain and range of functions such as these. In Functions and Function Notation , we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above.

Hp folio 9470m ultrabook specs

Since in this example,. After the graph is drawn, identify the domain and range for the function, and record it in your notes. So essentially any number if we're talking about reals when we talk about any number. Maths Games. We could try, let's do one more point over here. And, to get a flavor for this, I'm going to try to graph this function right over here. So, that's right there it's a point 1, 7 and it gives us a scaffold for what this parabola, what this curve will look like. DeWind plans to install carpet in every room of the house, with the exception of the square kitchen. Continue to adjust the values of the coefficients until the graph satisfies the domain and range values listed below. Let us have a step by step guidance on how to find the domain and range of a quadratic function. Does the shooter make the basket? Videos No videos. The student is expected to:.

There are four different common relationships between variables you're sure to run into: they're linear, direct, quadratic, and inverse relationships.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser. But, as you go to the right, as x values increase to the right or decrease to the left, then the parabola goes upwards. The domain of any quadratic function is all real numbers unless the context of the function presents some restrictions. Chris Irineo. About About this video Transcript. Commercial Maths. If you're seeing this message, it means we're having trouble loading external resources on our website. Flag Button navigates to signup page. Some functions, such as linear functions e. The student is expected to: A 6 A determine the domain and range of quadratic functions and represent the domain and range using inequalities Resource Objective s To determine the domain and range of a quadratic function when given a statement or graph. Think that you're tossing a baseball straight up in the air.