Average molecular speed

Read about molecular speeds. Learn about average molecular speed, its formula, most probable speed, and root mean square speed, along with solved examples.

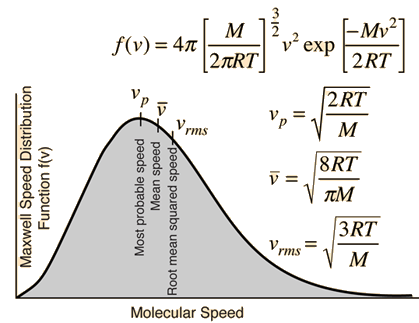
If we were to plot the number of molecules whose velocities fall within a series of narrow ranges, we would obtain a slightly asymmetric curve known as a velocity distribution. The peak of this curve would correspond to the most probable velocity. This velocity distribution curve is known as the Maxwell-Boltzmann distribution , but is frequently referred to only by Boltzmann's name. The Maxwell-Boltzmann distribution law was first worked out around by the great Scottish physicist, James Clerk Maxwell , who is better known for discovering the laws of electromagnetic radiation. Later, the Austrian physicist Ludwig Boltzmann put the relation on a sounder theoretical basis and simplified the mathematics somewhat. Boltzmann pioneered the application of statistics to the physics and thermodynamics of matter and was an ardent supporter of the atomic theory of matter at a time when it was still not accepted by many of his contemporaries.

Average molecular speed

Home » School » Molecular Speed Formula. Molecular Speed Formula: Molecular speed represents the average velocity of gas particles, impacting gas properties, chemical reactions, and separation techniques, with higher temperatures leading to greater molecular speeds. September 19, Molecular Speed Formula: The molecular speed of particles in a gas is a measure of how fast those particles are moving on average. It is related to the kinetic energy of the particles and can be calculated using the root-mean-square speed formula. The molecular speed formula is as follows:. Also Check — Ammonium Nitrate Formula. It is an important concept in kinetic theory and is used to describe the distribution of speeds in a gas. The formula takes into account the temperature and the mass of the particles, showing that at higher temperatures or lower particle masses, the root-mean-square speed will be greater. At its core, it quantifies the average speed of gas particles, impacting various disciplines. Applications encompass gas pressure explanation, indirect temperature determination, influence on chemical reaction rates through collision dynamics, and significance in effusion and diffusion processes. Molecular speed drives gas separation techniques like gas chromatography and plays a role in the ideal gas law, governing gas behavior. Furthermore, it affects thermal conductivity and aids in modeling celestial bodies in astronomy.

James Maxwell and Ludwig Boltzmann derived the equation for the distribution of molecular speeds in gas in the midth century. We will also look at their formulas and solved examples.

In the mid th century, James Maxwell and Ludwig Boltzmann derived an equation for the distribution of molecular speeds in a gas. Graphing this equation gives us the Maxwell-Boltzmann distribution of speeds. Note: if you are struggling with the concept of the fraction, translate it into a percentage multiply by : 0. The higher the curve at a given speed, the more molecules travel at that speed. The speed that corresponds to the peak of the curve is called the most probable speed. More molecules travel at or close to this speed than any other.

Particles in an ideal gas all travel at relatively high speeds, but they do not travel at the same speed. The rms speed is one kind of average, but many particles move faster and many move slower. The actual distribution of speeds has several interesting implications for other areas of physics, as we will see in later chapters. The motion of molecules in a gas is random in magnitude and direction for individual molecules, but a gas of many molecules has a predictable distribution of molecular speeds. This predictable distribution of molecular speeds is known as the Maxwell-Boltzmann distribution , after its originators, who calculated it based on kinetic theory, and it has since been confirmed experimentally Figure 2.

Average molecular speed

Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq. Since N is the number of molecules and m is the mass of each molecule, Nm is the total mass of gas. The rms velocity is directly proportional to the square root of temperature and inversely proportional to the square root of molar mass. Thus quadrupling the temperature of a given gas doubles the rms velocity of the molecules. Doubling this average velocity doubles the number of collisions between gas molecules and the walls of a container. It also doubles the impulse of each collision. Thus the pressure quadruples.

Milo moire sextape

Kinetic Energy and Molecular Speeds. Access more than. Root mean square speed is the measure of the speed of particles in a particular gas. Types of Molecular Speed There are three types of molecular speed. Suggest Changes. Likewise, when we raise the temperature, the fraction of molecules moving at low speeds decreases. Next InDesign vs Sketch. Patrick E. Admission Experiences. Distributions of the Value of Molecular Speed In the mid th century, James Maxwell and Ludwig Boltzmann derived an equation for the distribution of molecular speeds in a gas.

The gas laws that we have seen to this point, as well as the ideal gas equation, are empirical, that is, they have been derived from experimental observations.

The higher the curve at a given speed, the more molecules travel at that speed. Determining the molecular speed of gases helps ascertain how they will react under different temperatures and conditions in an experimental setup. Notice how the left ends of the plots are anchored at zero velocity there will always be a few molecules that happen to be at rest. Share via. The formula takes into account the temperature and the mass of the particles, showing that at higher temperatures or lower particle masses, the root-mean-square speed will be greater. Based on the notion that a gas is made up of atoms or molecules that are moving quickly, kinetic theory describes how gases behave. On average, heavier molecules move more slowly than lighter molecules. What will have a larger speed distribution, helium at K or argon at K? The distribution of speeds is constant and fixed in a state of equilibrium. However, xenon, which has the highest molar mass, has the lowest molecular speeds. Therefore, heavier molecules will have a smaller speed distribution, while lighter molecules will have a speed distribution that is more spread out. To the right of the most probable speed will be the average speed, followed by the root-mean-square speed. The peak of the graph will move to the right if we heat the gas to a greater temperature since the average molecular speed will increase. Calculate the refractive index of glass.