Altitude of a triangle definition

Triangles contain special segments like perpendicular bisector, median, and altitude, altitude of a triangle definition. When you think of altitude, you may think of the increasing elevations of mountain ranges; the term altitude also has its place in Geometry, however, and it refers to the height of a triangle. Explore our app and discover over 50 million learning materials for free. In this article, we will understand the concept of altitudes in triangles and their related terms in detail.

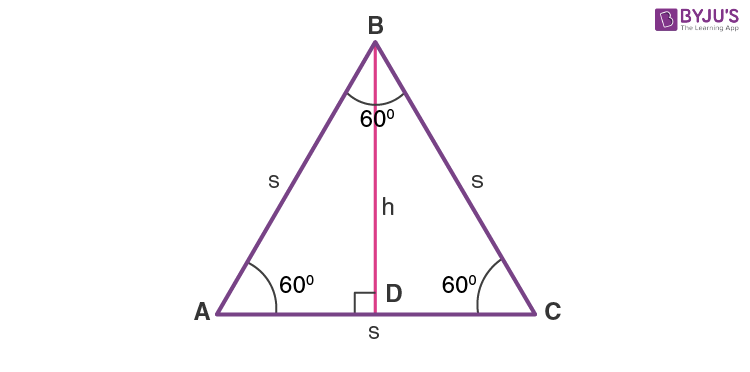
The altitude of a triangle is the perpendicular line segment drawn from the vertex to the opposite side of the triangle. It may lie inside or outside the triangle, based on the types of triangles. The altitude of a triangle basically defines the height, when we have to measure the area of a triangle, with respect to the base. The altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. Also, known as the height of the triangle, the altitude makes a right-angle triangle with the base.

Altitude of a triangle definition

In geometry , an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection. Altitudes can be used in the computation of the area of a triangle : one-half of the product of an altitude's length and its base's length equals the triangle's area. Thus, the longest altitude is perpendicular to the shortest side of the triangle. The altitudes are also related to the sides of the triangle through the trigonometric functions. In an isosceles triangle a triangle with two congruent sides , the altitude having the incongruent side as its base will have the midpoint of that side as its foot. Also the altitude having the incongruent side as its base will be the angle bisector of the vertex angle. It is common to mark the altitude with the letter h as in height , often subscripted with the name of the side the altitude is drawn to. In a right triangle , the altitude drawn to the hypotenuse c divides the hypotenuse into two segments of lengths p and q.

About altitude, different triangles have different types of altitude.

The altitude of a triangle is a line from a vertex to the opposite side, that is perpendicular to that side, as shown in the animation above. A triangle therefore has three possible altitudes. The altitude is the shortest distance from a vertex to its opposite side. The word 'altitude' is used in two subtly different ways: It can refer to the line itself. For example, you may see "draw an altitude of the triangle ABC".

The altitude of a triangle , or height , is a line from a vertex to the opposite side, that is perpendicular to that side. It can also be understood as the distance from one side to the opposite vertex. Every triangle has three altitudes h a , h b and h c , each one associated with one of its three sides. The three altitudes of a triangle or its extensions intersect at a point called orthocenter. The altitude can be inside the triangle , outside it, or even coincide with one of its sides, it depends on the type of triangle it is:.

Altitude of a triangle definition

The altitude of a triangle is a perpendicular that is drawn from the vertex of a triangle to the opposite side. Since there are three sides in a triangle, three altitudes can be drawn in it. Different triangles have different kinds of altitudes. The altitude of a triangle which is also called its height is used in calculating the area of a triangle and is denoted by the letter 'h'. The altitude of a triangle is the perpendicular line segment drawn from the vertex of the triangle to the side opposite to it. The altitude makes a right angle with the base of the triangle that it touches. It is commonly referred to as the height of a triangle and is denoted by the letter 'h'. It can be measured by calculating the distance between the vertex and its opposite side.

Chika yasumura

Table Of 4. Learn Practice Download. Denote the circumradius of the triangle by R. Read Edit View history. Rate Get App Share. Will you pass the quiz? Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. Now using the general formula of the area and equating it with Heron's formula we can obtain the altitude,. Save Article. Constructing the altitude of a triangle altitude inside. The altitude of a triangle basically defines the height, when we have to measure the area of a triangle, with respect to the base. Altitude is also known as. What is altitude?

A triangle is a closed, two-dimensional shape that has 3 sides, 3 angles, and 3 vertices. It is the polygon with the fewest sides. Since it is the simplest form of a polygon, any polygon can be constructed using two or more triangles.

Equilateral triangle altitude, StudySmarter Originals. Also the altitude having the incongruent side as its base will be the angle bisector of the vertex angle. Jetzt kostenlos anmelden. This is done by extending the base of the given obtuse triangle. Dover Publications, Inc. What is the altitude in a triangle? The altitude of a triangle is the line drawn from a vertex to the opposite side of a triangle. The orthocenter is the intersection point of altitudes. In the animation at the top of the page: Drag the point A and note the location of the altitude line. All the three altitudes of a triangle are concurrent; that is, they intersect at a point called the orthocenter. Right triangle Orthocenter, StudySmarter Originals. Is the altitude of an obtuse triangle inside the triangle?