A particle is rotating in a circle with uniform speed

Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed. For example, any point on a propeller spinning at a constant rate is executing uniform circular motion. Other examples are the second, minute, and hour hands of a watch.

Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed. For example, any point on a propeller spinning at a constant rate is executing uniform circular motion. Other examples are the second, minute, and hour hands of a watch. It is remarkable that points on these rotating objects are actually accelerating, although the rotation rate is a constant. To see this, we must analyze the motion in terms of vectors. In one-dimensional kinematics, objects with a constant speed have zero acceleration. However, in two- and three-dimensional kinematics, even if the speed is a constant, a particle can have acceleration if it moves along a curved trajectory such as a circle.

A particle is rotating in a circle with uniform speed

Views: 5, Views: 6, Connect with our Physics tutors online and get step by step solution of this question. Are you ready to take control of your learning? Class System of Particles and Rotational Motion. Uniform circular motion. Assertion: A particle is rotating in a circle with constant sp. Solving time: 2 mins. If both Assertion and Reason are true and the Reason is correct explanation of the Assertion. If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.

In the first diagram, let's say the object is a person sitting inside a plane, the two forces point down only when it reaches the top of the circle. B Constant in magnitude only.

Angular position and speed Uniform circular motion Centripetal force Rotational energy Angular momentum Problems Next topic Tutorial contents. This topic deals with a single mass performing a circular motion. We initially start with this simplified version, but it will need to be generalised because some problems in chemistry require a more sophisticated analysis. We first need a way of defining the position of a particle in its circular motion. We can use Cartesian coordinates, but these are not very convenient, the relationship between x and y on a circle of radius r is which has an unfortunate ambiguity of sign.

The learning objectives in this section will help your students master the following standards:. In addition, the High School Physics Laboratory Manual addresses content in this section in the lab titled: Circular and Rotational Motion, as well as the following standards:. Ask students to give examples of circular motion. Review linear acceleration. In the previous section, we defined circular motion.

A particle is rotating in a circle with uniform speed

This may be a good time to review Section 4. In particular, you should recall that even if the speed is constant, the acceleration vector is always non-zero in uniform circular motion because the velocity changes direction. The only way for the object to undergo uniform circular motion as depicted is if the net force on the object is directed towards the center of the circle. If the string is under tension, the force of tension will always be towards the center of the circle. The forces on the object are thus:. An object is undergoing uniform circular motion in the horizontal plane, when the string connecting the object to the center of rotation suddenly breaks. What path will the block take after the string broke? What is the maximum speed with which the car can go around the curve without skidding? If the car is going at constant speed around a circle, then the sum of the forces on the car must be directed towards the center of the circle.

Chair caning supplies

A runner taking part in the m dash must run around the end of a track that has a circular arc with a radius of curvature of The direction of the centripetal acceleration is toward the center of the circle. A fan is rotating at a constant In a non-uniform circular motion, normal force does not always point in the opposite direction of weight. The directions of centripetal and tangential accelerations can be described more conveniently in terms of a polar coordinate system, with unit vectors in the radial and tangential directions. A Point The equations of motion describe the movement of the center of mass of a body, which remains at a constant distance from the axis of rotation. From this result we see that the proton is located slightly below the x -axis. Because speed is constant, the velocity vectors on the right sweep out a circle as time advances. History Timeline Textbooks. Views: 6,

Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed.

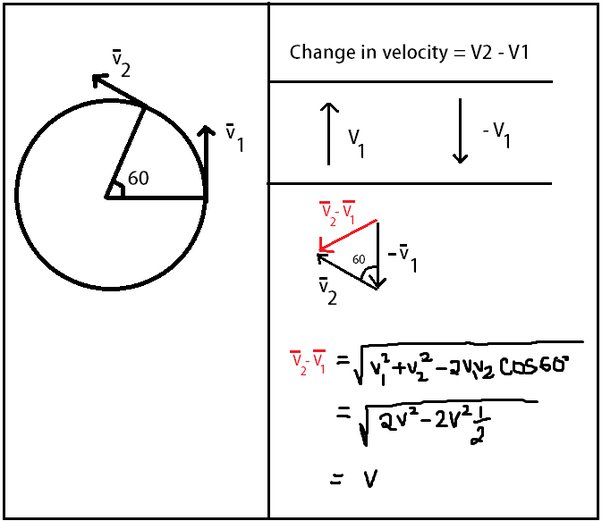
What is the magnitude of the acceleration of a point on one of its blades Assertion: A particle is rotating in a circle with constant sp. What is the acceleration of Venus toward the Sun, assuming a circular orbit? What is the angular momentum of the particle about O? Similarly the force required to make a satellite move in a circular orbit can only be gravitational attraction to the central planet. In a non-uniform circular motion, there are additional forces acting on the object due to a non-zero tangential acceleration. Stuck on the question or explanation? The rotation around a fixed axis of a three-dimensional body involves the circular motion of its parts. A particle undergoes uniform circular motion. In physics , uniform circular motion describes the motion of a body traversing a circular path at a constant speed. Which of the following graphs represents the correct relation between A and a when the ball goes from Q to R? Typical centripetal accelerations are given in the following table. The velocity vector is also shown and is tangent to the circle.