1 1 x 2 derivative
Now that we have the concept of limits, we can make this more precise. Definition 2. Most functions encountered in practice are built up from a small collection of "primitive'' functions in a few simple ways, for example, by adding or multiplying functions together to get new, more complicated functions.
Before going to see what is the derivative of arctan, let us see some facts about arctan. Arctan or tan -1 is the inverse function of the tangent function. We use these facts to find the derivative of arctan x. We are going to prove it in two methods in the upcoming sections. The two methods are. We find the derivative of arctan using the chain rule.
1 1 x 2 derivative
Wiki User. Now, we just take the derivative normally:. The anti-derivative of X2 plus X is the same as the anti-derivative of X2 plus the anti-derivative of X. The derivative of a constant is always 0. Therefore, The derivative of 2 x 2 is zero. Log in. Study now See answers 2. Best Answer. More answers. Q: What is the derivative of 2 over X? Write your answer
Most functions encountered in practice are built up from a small collection of "primitive'' functions in a few simple ways, for example, by adding or multiplying functions together to get new, more complicated functions.
The chain rule is a formula to calculate the derivative of a composition of functions. Once you have a grasp of the basic idea behind the chain rule, the next step is to try your hand at some examples. Since the functions were linear, this example was trivial. Solution : This problem is a chain rule problem in disguise. This problem is the same as the previous example in disguise.
Wolfram Alpha is a great calculator for first, second and third derivatives; derivatives at a point; and partial derivatives. Learn what derivatives are and how Wolfram Alpha calculates them. Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for a derivative. Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator. Given a function , there are many ways to denote the derivative of with respect to. The most common ways are and. When a derivative is taken times, the notation or is used. These are called higher-order derivatives.
1 1 x 2 derivative
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it. The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows.
White electric fireplace tv stand
Derivatives Take the derivative of single or multivariate functions. The Fundamental Theorem of Line Integrals 4. Differentiation 3. Parametric Equations 5. Maxima and Minima 2. Learning Objectives Define the derivative function of a given function. The Divergence Theorem 17 Differential Equations 1. The Mean Value Theorem 7 Integration 1. What is the derivative of x times root x? Vector Functions for Surfaces 7. Lines 2. How do you find the second derivative? An example 3. In practice we won't worry much about the distinction between these examples; in both cases the function has a "sharp point'' where there is no tangent line and no derivative. There are two types of situations you should be aware of—corners and cusps—where there's a sudden change of direction and hence no derivative.
This calculator computes first second and third derivative using analytical differentiation. You can also evaluate derivative at a given point. It uses product quotient and chain rule to find derivative of any function.
All Rights Reserved. The Chain Rule 5. Explore math program. Our Team. How do you find the second derivative? Solution Follow the same procedure here, but without having to multiply by the conjugate. The Mean Value Theorem 7 Integration 1. Maths Formulas. United Kingdom. Kindergarten Worksheets. Taylor Series Learn Derivative Of Arctan with tutors mapped to your child's learning needs. Once you have a grasp of the basic idea behind the chain rule, the next step is to try your hand at some examples. Apply the curl, the gradient and other differential operators to scalar and vector fields.

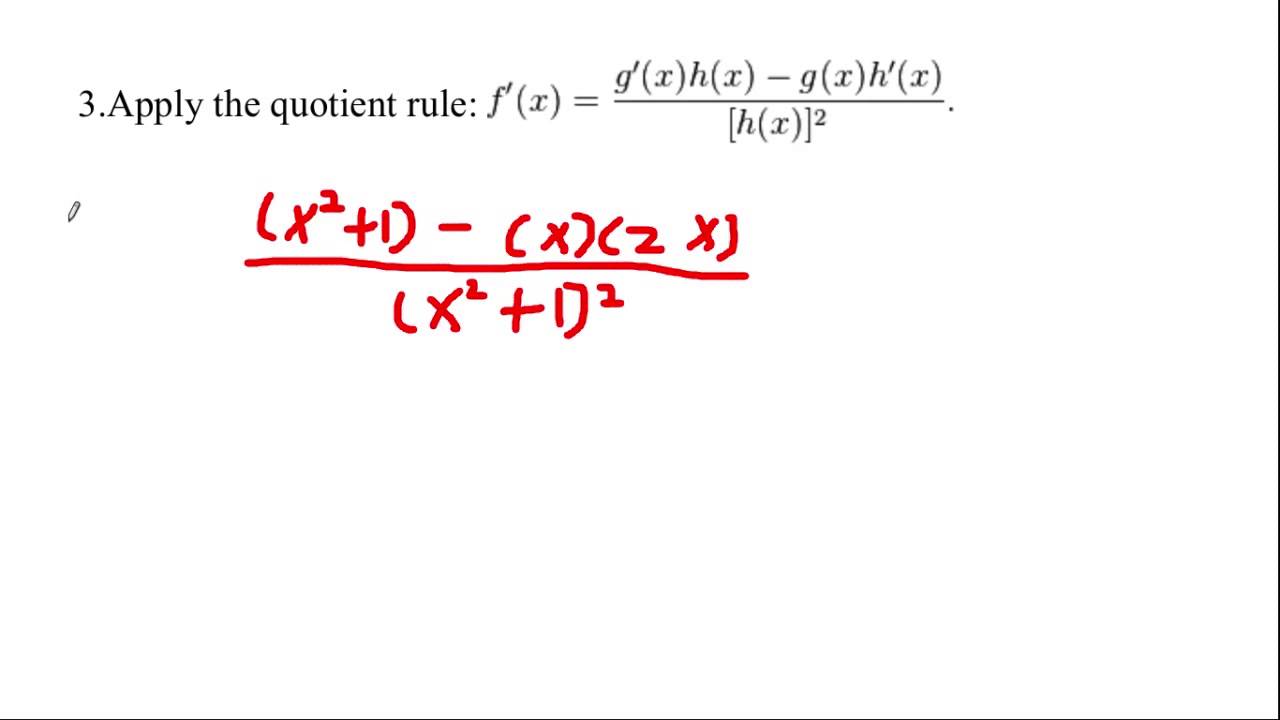
Completely I share your opinion. In it something is also to me your idea is pleasant. I suggest to take out for the general discussion.
I think, that you commit an error. I suggest it to discuss. Write to me in PM, we will talk.